Проекция силы на ось и на плоскость.
Перейдем к рассмотрению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проекции данной силы на любые параллельные и одинаково направленные оси равны друг другу. Этим удобно пользоваться при вычислении проекции силы на ось, не лежащую в одной плоскости с силой.
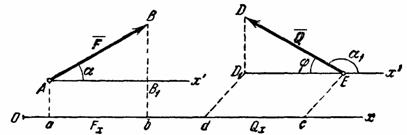
Рис. 12
Обозначать проекцию силы  на ось Ох будем символом
на ось Ох будем символом 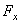 . Тогда для сил, изображенных на рис. 12, получим:
. Тогда для сил, изображенных на рис. 12, получим:
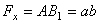 ,
, 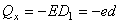 .
.
Но из чертежа видно, что 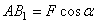 ,
, 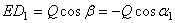 .
.
Следовательно,
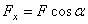 ,
, 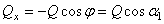 ,
,
т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпендикулярна к оси, то ее проекция на ось равна нулю.
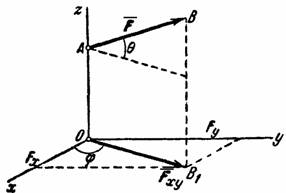
Рис.13
Проекцией силы  на плоскость Оху называется вектор
на плоскость Оху называется вектор 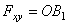 , заключенный между проекциями начала и конца силы
, заключенный между проекциями начала и конца силы  на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим численным значением, но и направлением в плоскости Оху. По модулю
на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим численным значением, но и направлением в плоскости Оху. По модулю 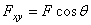 , где
, где 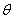 — угол между направлением силы
— угол между направлением силы  и ее проекции
и ее проекции 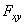 .
.
В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроектировать на данную ось. Например, в случае, изображенном на рис. 13, найдем таким способом, что
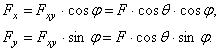
Дата добавления: 2015-08-08; просмотров: 891;
