Групповая скорость. Формула Рэлея

В природе не бывает строго монохроматических волн, так как идеальная монохроматическая волна должна существовать неограниченно долго во времени. Реальные волны излучаются в течение определенного интервала времени. На практике часто используют электромагнитные волны в виде импульсов. Одиночный импульс (рис. 73.1), используя преобразование Фурье, можно представить как совокупность различных монохроматических волн . 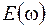Такую совокупность называют волновым пакетом, или группой волн. Точку, в которой амплитуда имеет максимальное значение, называют центром группы волн (точка 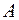). Скорость перемещения центра группы волн (волнового пакета) называется групповой скоростью 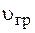. Групповая скорость – это скорость, с которой переносится энергия волнового пакета. Можно показать, что групповая скорость определяется выражением

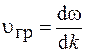. (73.1)

Введенное в § 23 понятие фазовой скорости применительно к волновому пакету теряет смысл, так как само понятие фазы применимо только для монохроматических волн. Так как каждая из монохроматических волн, образующих группу, распространяется в диспергирующей среде с различной скоростью, то волновой пакет по мере продвижения в среде будет искажаться (расплываться).

Для монохроматической волны . Подставляя это выражение в (73.1), получим 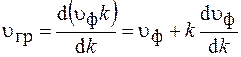. Переходя от волнового числа 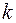к длине волны 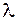с учетом того, что 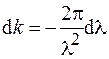, получим формулу Рэлея, которая связывает групповую и фазовую скорости

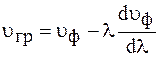. (73.2)

Для монохроматической волны групповая и фазовая скорости совпадают. Для реального ограниченного во времени сигнала они различны и только групповая скорость имеет физический смысл. В соответствии с теорией относительности никакой материальный сигнал (частица или волна) не может распространяться со ско­ростью, большей скорости света, поэтому групповая скорость всегда меньше скорости света:

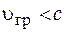. (73.3)

Фазовая скорость может быть как больше скорости света, так и меньше. В этом нет никакого противоречия с теорией относитель­ности именно потому, что фазовая скорость не связана с переносом энергии и информации.