Элементарная теория дисперсии

При распространении электромагнитной волны в непроводящей среде (диэлектрике) электромагнитное поле вызывает вынужденные колебания электронов в атомах (молекулах) вещества. Строгий анализ взаимодействия ЭМВ с частицами вещества возможен только на основе квантовой механики. Однако некоторые характерные особенности могут быть качественно описаны в рамках более простой классической модели.

Будем считать, что электрон в атоме вращается вокруг ядра по стационарной круговой орбите и удерживается на ней некоторой упругой силой, природа которой в рамках элементарной теории не имеет значения. Отклонение электрона от стационарной орбиты будем характеризовать смещением 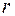. В результате взаимодействия с плоской монохроматической волной электрон будет совершать вынужденные колебания около стационарной орбиты, которые в соответствии со вторым законом Ньютона должны удовлетворять дифференциальному уравнению

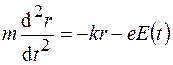, (74.1)

где 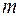– масса электрона; 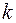– коэффициент жесткости упругой связи; 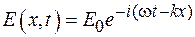– напряженность электрического поля монохроматической волны; 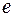– заряд электрона. Вынужденные колебания совершаются с частотой вынуждающей силы 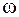, поэтому решение дифференциального уравнения будем искать в виде 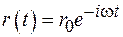. Подставляя это решение в (74.1), после элементарных преобразований приведем его к виду

.

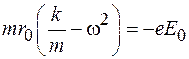Обозначив 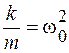, выразим из полученного уравнения амплитуду вынужденных колебаний:

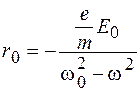. (74.2)

Колебания электрона приведут к возникновению дипольного момента :

. (74.3)

Если в единице объема вещества содержится 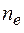электронов, то поляризованность среды 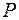будет равна

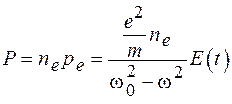. (74.4)

Диэлектрическая восприимчивость среды 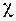определяется отношением поляризованности к напряженности поля, поэтому

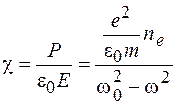. (74.5)

Используя известные соотношения между диэлектрической восприимчивостью 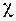, проницаемостью 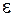и показателем преломления , для немагнитной среды ( 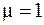) из последнего выражения получим

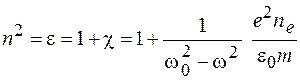. (74.6)

Если частота электромагнитной волны 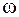существенно отличается от частоты собственных колебаний электрона в атоме 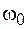, то вторым слагаемым в правой части выражения (74.6) можно пренебречь, и показатель преломления будет близок к единице. При этом с увеличением частоты показатель преломления монотонно возрастает, что соответствует области нормальной дисперсии.

Вблизи резонансной частоты ( 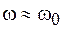) второе слагаемое в (74.6) неограниченно возрастает по модулю, т. е. зависимость 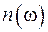имеет разрыв на резонансной частоте. Это происходит потому, что в уравнении (74.1) не учтены потери энергии. В отсутствие потерь амплитуда вынужденных колебаний при резонансе неограниченно возрастает, однако в любой реальной колебательной системе всегда имеются потери энергии.

Более строгий анализ взаимодействия электромагнитной волны с частицами вещества с учетом потерь приводит к зависимости показателя преломления от частоты, приведенной на рисунке 74.1.

Из графика видно, что вдали от резонансной частоты 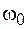показатель преломления по-прежнему возрастает с увеличением частоты (нормальная дисперсия). Однако вблизи резонансной частоты показатель преломления уменьшается, и эта область соответствует аномальной дисперсии. В области аномальной дисперсии, ограниченной на рисунке пунктирными линиями, наблюдается поглощение излучения, причем коэффициент поглощения 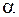принимает максимальное значение вблизи резонансной частоты .

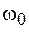В атоме вещества имеется несколько электронов (за исключением водорода) и они могут находиться на разных орбитах, поэтому в спектре поглощения имеется не одна, а большое число линий поглощения и в пределах каждой такой линии наблюдается аномальная дисперсия.

Таким образом, оптические свойства вещества (скорость распространения, показатель преломления, коэффициент отражения и поглощения) определяются взаимодействием электромагнитной волны с электронами вещества и зависят от частоты (длины волны). В результате этого взаимодействия происходит резонансное поглощение энергии электромагнитной волны, что приводит к ее затуханию по мере распространения в веществе.