Дифракция Фраунгофера на узкой щели

Пусть препятствие в виде узкой длинной щели освещается плоской монохроматической волной, которая распространяется вдоль оси 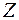перпендикулярно плоскости щели (рис. 57.1). Найдем распределение интенсивности в картине дифракции Фраунгофера, наблюдаемой на экране, расположенном на расстоянии 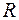за щелью. Для этого разобьем поверхность щели на узких полосок, параллельных краям щели и имеющих равную ширину. Амплитуду волны, приходящей в точку наблюдения от полоски с номером i, будем изображать век тором 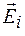. В центр дифракционной картины (точку О на рисунке 57.2, а) волны от всех полосок будут приходить в одинаковой фазе, поэтому векторная диаграмма будет выглядеть так, как показано на рисунке 57.2, б. Обозначим результирующую амплитуду в этом случае как 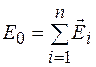, а соответствующую интенсивность – .

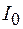В точку 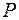, смещенную на расстояние 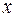относительно центрального максимума (рис. 57.3, а), от щели будет приходить плоская волна, распространяющаяся под углом . При этом волны, приходящие от пары смежных полосок, отличаются по фазе на постоянную величину 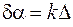, где 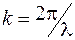– волновое число; 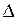– оптическая разность хода волн для двух смежных полосок. Векторная диаграмма для внеосевой точки будет представлять собой часть правильного многоугольника, вписанного в окружность радиусом 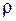(рис. 57.3, б). Угловой размер дуги окружности 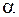определяется разностью хода волн от краев щели 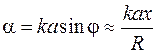. Результирующая амплитуда 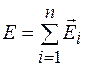изобразится хордой, стягивающей дугу окружности длиной 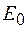. Из прямоугольного треугольника получим 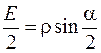. Длина дуги 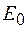связана с радиусом окружности и углом соотношением 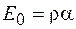. Отсюда для результирующей амплитуды находим

. (57.1)

Поскольку интенсивность пропорциональна квадрату амплитуды, то ее распределение в дифракционной картине определяется выражением

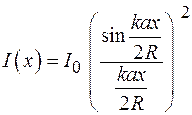, (57.2)

где 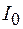– интенсивность в центре дифракционной картины.

Дифракционная картина имеет вид чередующихся темных и светлых полос, параллельных щели (рис. 57.4). В центре картины находится светлая полоса. По мере удаления от центра интенсивность светлых полос быстро уменьшается. Координаты минимумов интенсивности определяются из условия :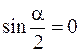

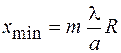, (57.3)

где 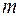– целое число, называемое порядком дифракционного минимума. Ширина полос (расстояние между двумя смежными минимумами) зависит от длины волны, размеров отверстия и расстояния до экрана:

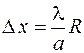. (57.4)