Метод зон Френеля. Френель первым предложил метод анализа картин дифракции, который получил название метода зон Френеля

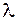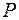Френель первым предложил метод анализа картин дифракции, который получил название метода зон Френеля. Пусть монохроматическая волна с длиной распространяется от точечного источника в точку наблюдения (рис. 54.1). На пути распространения волны установлен непрозрачный экран 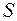с круглым отверстием радиусом 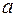. Построим волновую поверхность радиусом , где – расстояние от источника до плоскости экрана. Из точки наблюдения Р, удаленной от плоскости экрана на расстояние 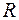, построим сферы радиусами 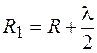, , 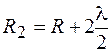, 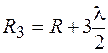..., 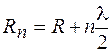, где – номер сферы. Эти сферы пересекутся с волновой поверхностью по окружностям, радиусы которых обозначим 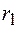, , 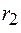..., 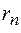, и разобьют ее (волновую поверхность) на кольцевые зоны, которые называются зонами Френеля. Из построения следует, что расстояние от границ двух соседних зон Френеля до точки наблюдения 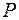равно 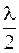, а это означает, что вторичные волны от двух соседних зон Френеля приходят в точку наблюдения с разностью фаз 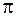. Обозначим амплитуды этих волн 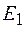, , 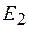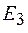и т. д. Тогда амплитуда 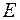результирующей волны в точке наблюдения

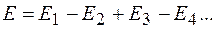(54.1)

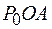Чередование знаков в (54.1) отражает указанную разность фаз . Из треугольников и 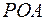найдем радиус зоны Френеля с номером . По теореме Пифагора можно записать

,

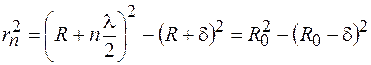откуда с точностью до бесконечно малых величин второго порядка найдем 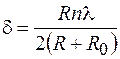, где 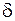– длина отрезка (расстояние от вершины волновой поверхности до точки 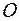). Подставляя найденное значение 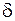в выражение для радиуса зоны Френеля 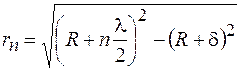и вновь отбрасывая бесконечно малые второго порядка, получим окончательно для радиуса -й зоны Френеля выражение

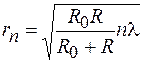. (54.2)

Когда источник удален в бесконечность ( 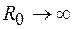), т. е. отверстие освещается плоской монохроматической волной, из формулы (54.2) получим

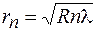. (54.3)

Если положить 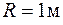, 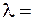0,5 мкм, то для радиуса первой зоны Френеля получим значение 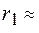0,7 мм. Эта оценка показывает, что радиусы зон Френеля для видимого света достаточно малы, однако при увеличении длины волны или расстояния до точки наблюдения размеры зон Френеля увеличиваются.

Можно показать, что для малых площади зон Френеля примерно равны. Отсюда можно сделать вывод, что амплитуды 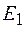, , 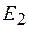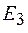и т. д. также примерно равны друг другу. Запишем выражение (54.1) в виде

.

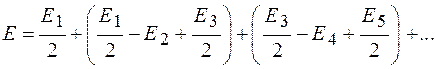Слагаемые в скобках приблизительно равны нулю, поэтому из последнего выражения следует, что бесконечный ряд (54.1)

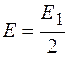. (54.4)

Полученное соотношение показывает, что амплитуда волны от первой зоны Френеля в 2 раза больше амплитуды волны при полностью открытом волновом фронте. Следовательно, если на пути волны поставить непрозрачный экран с круглым отверстием, радиус которого равен радиусу первой зоны Френеля, интенсивность света в точке наблюдения возрастет в 4 раза.

Если размер отверстия равен радиусу второй зоны Френеля, то амплитуда волны в точке наблюдения будет определяться первыми двумя слагаемыми в (54.1), и с учетом того, что они примерно равны друг другу, будет близка к нулю. Следовательно, если в отверстии укладывается две зоны Френеля, то в точке наблюдения будет темное пятно (минимум интенсивности). Рассуждая подобным образом, приходим к общему выводу: если в отверстии, на котором дифрагирует волна, укладывается нечетное число зон Френеля, то в точке наблюдения будет максимум интенсивности; если же число зон четное, то интенсивность имеет минимальное значение.