Дифракция Фраунгофера и Френеля

Распределение амплитуды волны в плоскости наблюдения зависит от размеров и формы препятствия, на котором происходит дифракция. Аналитический расчет дифракционной картины в общем случае представляет сложную математическую задачу. Сложность решения задачи дифракции волн во многом зависит от числа зон Френеля, укладывающихся на препятствии, и в зависимости от этого различают дифракцию Фраунгофера и дифракцию Френеля.

Дифракция Фраунгофера имеет место, если размеры препятствия 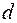много меньше радиуса первой зоны Френеля как со стороны источника, так и со стороны плоскости наблюдения, т. е.

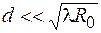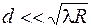и . (55.1)

Это будет в том случае, если источник и точка наблюдения находятся достаточно далеко от препятствия, на котором происходит дифракция. При большом удалении источника можно считать, что приходящая от него волна является плоской. Таким же образом вторичные сферические волны, приходящие в удаленную точку наблюдения, можно считать плоскими. Поэтому говорят, что дифракция Фраунгофера наблюдается в параллельных пучках или в дальней зоне. При этом понятие дальней зоны определяется условием (55.1). Распределение интенсивности продифрагированной волны в плоскости наблюдения называют картиной дифракции Фраунгофера.

Когда источник или точка наблюдения находятся на близком расстоянии от препятствия так, что условие (55.1) не выполняется, то имеет место дифракция Френеля. В этом случае пренебрегать сферичностью падающей или продифрагированной волны уже нельзя и поэтому говорят, что дифракция Френеля наблюдается в сходящихся (или расходящихся) пучках. Распределение интенсивности продифрагированной волны в ближней зоне называется картиной дифракции Френеля. Ее анализ оказывается более сложным, чем при дифракции Фраунгофера.

Дифракция Фраунгофера определяет распределение амплитуды (и интенсивности) волны, т. е. диаграмму направленности передающей антенны, в дальней зоне. Распределение поля в ближней зоне определяется дифракцией Френеля на апертуре антенны.