Дифракция Френеля на краю полуплоскости

Если препятствие на пути плоской волны представляет собой непрозрачную полуплоскость, приближение Фраунгофера для анализа картины дифракции оказывается недостаточным. Это следует из того, что при любом конечном расстоянии до плоскости наблюдения в пределах препятствия будет укладываться бесконечное число зон Френеля. Строгое решение задачи дифракции Френеля на краю полуплоскости показывает, что вблизи области геометрической тени картина представляет собой ряд чередующихся темных и светлых полос, параллельных краю полуплоскости и расположенных в освещенной области (рис. 58.1). В области тени интенсивность монотонно уменьшается до нуля, причем на границе геометрической тени, которая на рисунке соответствует 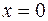, интенсивность в 4 раза меньше интенсивности падающей волны.

Качественно характер дифракционной картины можно пояснить с помощью векторной диаграммы. Пусть точка наблюдения 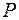находится в освещенной части на расстоянии x от края полуплоскости (рис. 58.2). Разобьем плоскость препятствия на узкие полоски, параллельные краю полуплоскости, так, чтобы разность хода от краев каждой полоски была постоянной и равной некоторой малой величине 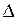. По мере удаления полоски от точки 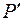амплитуда элементарного колебания будет постепенно уменьшаться, а изображающий вектор будет поворачиваться на угол 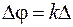вследствие увеличения оптической разности хода. Элементарные векторы от всех полосок, расположенных справа от точки наблюдения в освещенной части, образуют скручивающуюся спираль (спираль Корню), изображенную на рисунке в первом квадранте.

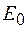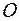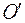Если бы препятствие на пути волны отсутствовало, то полоски, расположенные слева от точки наблюдения образовали бы вторую часть спирали, изображенную в третьем квадранте, и тогда амплитуда результирующего колебания представлялась бы вектором, соединяющим полюса спирали (точки и ). Но так как непрозрачная часть полуплоскости закрывает полоски, начиная с номера 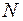, то из векторной диаграммы следует исключить соответствующие им элементарные векторы. Таким образом, каждая точка спирали соответствует определенной точке наблюдения с координатой 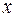, причем нижняя ветвь спирали соответствует 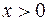(т. е. точкам наблюдения, расположенным справа от края полуплоскости), а верхняя ветвь – 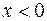. Амплитуда результирующего колебания изображается вектором, проведенным из соответствующей точки 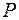спирали к полюсу 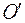. Начало координат соответствует точке наблюдения, расположенной на границе геометрической тени. Перемещая точку 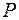по спирали от 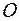к 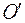, можно проследить за изменениями амплитуды и интенсивности.

При распространении радиоволн от передающей антенны к приемной вдоль земной поверхности линия горизонта играет роль края полуплоскости. В результате дифракции волна огибает земную поверхность и при достаточной мощности сигнала становится возможной загоризонтная связь. Если же передатчик и приемник находятся в пределах прямой видимости над линией горизонта, то дифракция приводит к заметным изменениям уровня принимаемого сигнала при 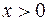, как показано на рисунке 58.1. Подобная ситуация возникает, например, когда спутник-ретранслятор выходит из-за горизонта.