Дифракция на многих щелях. Дифракционная решетка

Дифракционная решетка представляет собой устройство, осуществляющее пространственное периодическое изменение (модуляцию) падающей электромагнитной волны по амплитуде или фазе. Обычно решетка представляет собой совокупность большого числа параллельных штрихов, нанесенных на подложку из стекла или какого-либо полимерного материала. Решетки бывают пропускающие и отражательные. Простейшая пропускающая решетка представляет собой совокупность чередующихся прозрачных щелей шириной 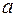, разделенных непрозрачными промежутками шириной 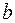(рис. 59.1, а). Такая решетка осуществляет пространственную модуляцию амплитуды падающей волны. Кроме амплитудных решеток применяют также фазовые решетки, которые осуществляют периодическое изменение фазы волны. Пример такой решетки, предложенный Майкельсоном, изображен на рисунке 59.1, б. Отражательные решетки имеют обычно треугольный профиль штриха. На поверхность такой решетки нанесено зеркальное покрытие, и они осуществляют модуляцию отраженной волны (рис. 59.1, в). Расстояние 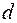между двумя соседними штрихами называется периодом решетки.

Пусть на пути плоской монохроматической волны установлена дифракционная решетка, изображенная на рисунке 59.1, а. В результате дифракции в плоскости наблюдения, расположенной на расстоянии 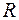от плоскости решетки, возникнет дифракционная картина, которая имеет вид чередующихся темных и светлых полос, параллельных штрихам решетки. В зоне дифракции Фраунгофера распределение интенсивности имеет вид

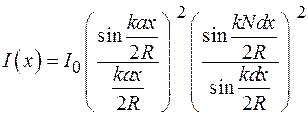, (59.1)

где 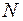– общее число штрихов решетки; 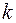– волновое число; 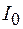– интенсивность в центре картины. На рисунке 59.2 приведен график зависимости 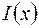. Из выражения (59.1) видно, что форма распределения 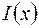определяется двумя сомножителями в скобках, первый из которых характеризует дифракцию на одном штрихе решетки (см. формулу (57.2)). На рисунке 59.2 этому сомножителю соответствует пунктирная кривая. Наличие второго сомножителя приводит к тому, что дифракционная картина имеет вид чередующихся максимумов и минимумов, вписанных в пунктирную кривую.

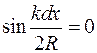Среди максимумов можно выделить главные максимумы, положение которых определяется условием . Это условие выполняется, если 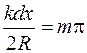. С учетом того, что 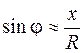, где 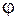– угол дифракции, под которым наблюдается соответствующий максимум, условие главных максимумов можно записать в виде

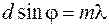, (59.2)

где 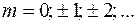– порядок главного максимума. При выполнении условия (59.2) второй сомножитель в (59.1) имеет неопределенность вида , раскрывая которую по правилу Лопиталля, получим

.

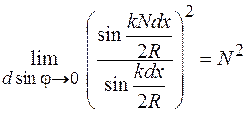Отсюда видно, что интенсивность главных максимумов в раз больше амплитуды соседних вторичных максимумов. Между главными максимумами расположены 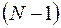минимумов, в которых интенсивность света равна нулю. Положение минимумов определяется условием 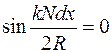. Угловое расстояние 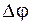между двумя соседними минимумами определяется длиной волны и числом штрихов решетки:

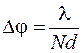. (59.3)

Выясним физический смысл условия образования главных максимумов (59.2). Для этого рассмотрим лучи, идущие из крайних точек двух смежных щелей в главный максимум 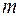-го порядка под углом 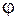, определяемом выражением (59.2). Из рисунка 59.3 видно, что эти лучи имеют оптическую разность хода и при условии (59.2) будут приходить в точку наблюдения в одной фазе. Это означает, что излучение от всех 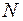штрихов приходит в точку главного максимума в одной фазе и в результате интерференции усиливается по амплитуде в 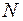раз. Таким образом, главные максимумы дифракционной картины наблюдаются в направлениях, для которых разность хода от двух крайних точек смежных штрихов равна целому числу длин волн.

Если на дифракционную решетку падает не монохроматическая волна, а излучение в интервале длин волн от 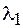до 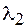, то для разных длин волн главный максимум 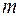-го порядка будет находиться в разных положениях. Таким образом, дифракционная решетка разлагает падающий свет в спектр, т. е. работает как спектральный прибор. Это свойство дифракционной решетки характеризуется двумя параметрами: угловой дисперсией и разрешающей способностью. Угловая дисперсия 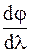равна отношению углового расстояния 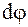между главными максимумами 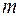-го порядка для двух длин волн к раз­ности этих длин волн . Из (59.2) легко получить 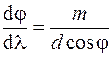или для малых углов дифракции

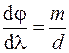. (59.4)

Из полученного выражения следует, что чем выше порядок 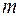спектра и чем меньше период решетки 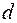, тем выше угловая дисперсия и тем больше расстояние между двумя спектральными линиями, различающимися по длине волны на .

В соответствии с критерием Рэлея две спектральные линии считаются разрешаемыми, если максимум дифракционного изображения одной из них совпадает с первым дифракционным минимумом другой (рис. 59.4). Разрешающей способностью 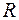дифракционной решетки называется отношение длины волны 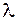к разности длин волн двух спектральных линий, разрешаемых по критерию Рэлея, т. е.

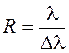. (59.5)

Из (59.1) следует, что угловое расстояние 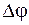между главным максимумом в спектре 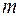-го порядка и первым дифракционным минимумом составляет 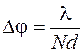. Тогда в соответствии с критерием Рэлея

,

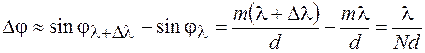откуда получим

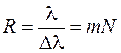. (59.6)

Таким образом, разрешающая способность дифракционной решетки прямо пропорциональна порядку 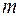спектра, в котором наблюдаются спектральные линии, и числу штрихов решетки .

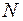Из (59.2) видно, что максимальный порядок спектра 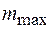, в котором можно наблюдать спектральную линию с длиной волны 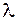, ограничен условием 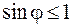и равен

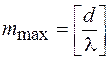, (59.7)

где 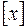– целая часть числа 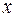. Современная промышленность выпускает различные типы дифракционных решеток, которые имеют до 2 400 штрихов/мм, при этом общее число штрихов 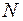может составлять до 100 000, а рабочие порядки спектра – от 1 до 6.