Диполь в электрическом поле

Рассмотрим действие на жесткий диполь однородного электрического поля (рис. 44.1).

На каждый заряд диполя электрическое поле действует: на положительный - с силой в направлении поля; на отрицательный - с силой 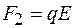в противоположном направлении. В однородном поле 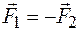. Поэтому эти силы образуют пару сил с плечом

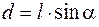, (44.1)

где α – угол между направлениями векторов 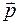и 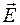. Пара сил создает вращающий момент

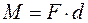. (44.2)

Так как 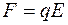, то, учитывая формулу (44.1), выражение (44.2) записываем в виде

.

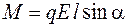Поскольку 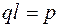- электрический момент диполя, то получаем

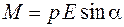. (44.3)

Это выражение представляет собой модуль векторного произведения векторов 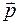и 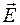, поэтому для вектора 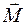следует записывать

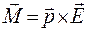. (44.4)

Однородное электрическое поле стремится ориентировать диполь в направлении поля, т. е. расположить его так, чтобы вектор 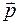совпал с направлением вектора 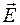(рис. 44.2). В этом случае на заряды действуют силы 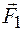и 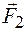, растягивающие диполь. В очень сильных полях может произойти разрыв связи между зарядами диполя и они станут свободными. Если это относится к молекулам диэлектрика, то в нем появляются свободные электрические заряды и возникает электрический ток - происходит пробой диэлектрика.

При изменении направления поля положение диполя также изменится. Если диполь помещен в переменное электрическое поле, то он там будет совершать колебательное движение относительно некоторого положения равновесия.

Пусть теперь диполь находится в неоднородном электрическом поле, напряженность которого возрастает в направлении оси Х (рис. 44.3). Из рисунка следует, что , поэтому 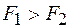и 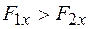. Тогда можно найти равнодействующую сил , направленную вдоль оси Х и перемещающую диполь в область более сильного поля при одновременном повороте диполя по часовой стрелке. Это будет в том случае, если угол a острый. Если диполь расположить так, что угол a тупой, то диполь будет поворачиваться и одновременно двигаться поступательно в противоположном направлении, т. е. в область более слабого поля до тех пор, пока угол a не станет острым. После этого происходит движение в область более сильного поля.

Найдем потенциальную энергию, которой обладает диполь во внешнем электрическом поле. Для этого определим работу, совершаемую внешними силами при повороте диполя, используя выражения (13.9) и (44.3):

.

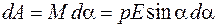Учитываем, что совершенная работа равна приращению потенциальной энергии 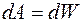, и получаем

.

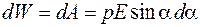Производим интегрирование полученного выражения

,

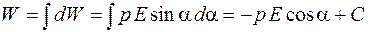где С - постоянная интегрирования, значение которой зависит от начальных условий. Для удобства выбирают 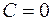, и выражение энергии диполя принимает вид

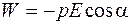. (44.5)

Из этой формулы следует:

1) если 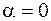, то , диполь обладает минимальнойэнергией, т. е. находится в состоянии устойчивого равновесия;

2) если 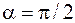, то ;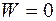

3) если 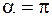, то 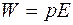, т. е. энергия диполя максимальна и он находится в состоянии неустойчивого равновесия.

Выражение (44.5) для энергии диполя получено для случая, когда он находится в однородном электрическом поле. Однако эта формула справедлива и для неоднородного поля.