Теория устойчивости гидрофобных дисперсных систем ДЛФО
Современная физическая теория коагуляции электролитами основана на общих принципах статистической физики, теории молекулярных сил и теории растворов. Ее авторами являются: Б.В. Дерягин, Л.Д. Ландау (1937-1941), Э. Фервей, Я. Овербек (по первым буквам ДЛФО).
Суть теории: между любыми частицами при их сближении возникает расклинивающее давление разделяющей жидкой прослойки в результате действия сил притяжения и отталкивания. Расклинивающее давление является суммарным параметром, учитывающим действие как сил притяжения, так и сил отталкивания.
Состояние системы зависит от баланса энергии притяжения (Uпр) и энергии отталкивания (Uотт). Преобладает Uотт – устойчивая система. Преобладает Uпр - нарушение агрегативной устойчивости – коагуляция.
Изменение энергии взаимодействия между двумя частицами при их сближении изображают графически (рис. 5.3).
Суммарную энергию системы из двух частиц (кривая 3) получают сложением Uотт и Uпр:
U=Uотт+Uпр = 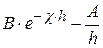
где: В – множитель, зависящий от значений электрических потенциалов ДЭС, свойств среды, температуры;
е – основание натурального логарифма;
c – величина, обратная толщине диффузного слоя;
h – расстояние между частицами;
А – константа молекулярных сил притяжения.
| |||||
 | |||||
| |||||
| |||||
Рис.5.3. Потенциальные кривые взаимодействия
коллоидных частиц:
1 – изменение энергии отталкивания с расстоянием;
2 – изменение энергии притяжения;
3 – результирующая кривая.
Рассмотрим результирующую кривую 3 на рис.5.3. На ней имеются характерные участки:
- В области малых расстояний имеется глубокий первичный минимум (потенциальная яма) – значительно преобладает Uпр. Первичный минимум отвечает непосредственному слипанию частиц (I).
- В области больших расстояний - вторичный неглубокий минимум (вторая потенциальная яма, отвечает притяжению через прослойку среды). На схеме II.
- В области средних расстояний на кривой имеется максимум и, если он расположен над осью абсцисс, то появляется энергетический барьер сил отталкивания (DUб).
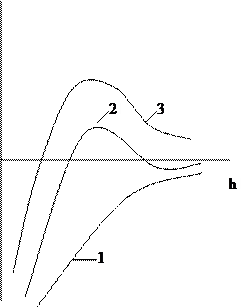
Результирующая кривая 3 может иметь различный вид в зависимости от устойчивости дисперсной системы (рис.5.4.).
| |||
 | |||
| |||
Рис. 5.4. Потенциальные кривые для определенных
состояний устойчивости дисперсной системы:
1 - в системе при любом расстоянии между частицами преобладает энергия притяжения над энергией отталкивания. В такой системе наблюдается быстрая коагуляция с образованием агрегатов.
2 - достаточно высокий потенциальный барьер и наличие вторичного минимума. Частицы взаимодействуют, но не имеют непосредственного контакта и разделены прослойками среды.
3 - система с высокой агрегатной устойчивостью (высокий потенциальный барьер и отсутствие вторичного минимума или при его глубине, меньшей тепловой энергии kТ).
В зависимости от высоты энергетического барьера и глубины потенциальных ям возможны различные варианты поведения частиц при сближении (рис.5.5), частицы обладают кинетической энергией – kТ.
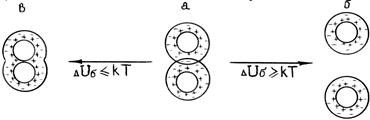
Рис.5.5. Схемы взаимодействия коллоидных частиц
| Состояние в: Малая высота барьера и неглубокий вторичный минимум: DUб@DUя£kT частицы вступают в ближнее взаимодействие, т.е. непосредственно соприкасаются – наступает коагуляция | Состояние а: Характеризуется тем, что перекрываются диффузные слои и сохранены прослойки среды между частицами (гели). Энергетический барьер довольно высок [DUб=(5-10)kT] вторичный минимум неглубок: DUя³kT Взаимодействующие частицы не могут разойтись (удерживают силы притяжения) и не могут приблизиться вплотную (препятствуют силы отталкивания). Добавление электролита чаще всего приводит к коагуляции (уменьшается h). | Состояние б: Высокий энергетический барьер DUб³kT и отсутствие или неглубокий вторичный минимум DUя£kT: Частицы не могут преодолеть барьер и расходятся без взаимодействия. Такая система агрегативно устойчива. |
Дисперсная система агрегативно устойчива при высоком энергетическом барьере сил отталкивания.
Дата добавления: 2015-08-08; просмотров: 3434;
