Идеал газ заңдары
Идеал газдар бағынатын заңдар әлдеқашан ашылған болатын. Бұл заңдардың барлығын да кинетикалық теория теңдеуінен шығарып алуға болады.
Бойль-Мариотт заңы.Газды тұрақты температура кезінде қарастырсақ, мұндай шарттар изотермиялық деп аталады. Егер (10.9) теңдеуінде 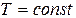 деп алатын болсақ, онда теңдіктің оң жағының тұрақты болып шығатындығы анық, яғни
деп алатын болсақ, онда теңдіктің оң жағының тұрақты болып шығатындығы анық, яғни 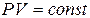 (10.11). Бұл теңдеуді изотерма теңдеуі деп атайды және ол Бойль-Мариотт заңының математикалық өрнегі болып табылады: газдың берілген массасы үшін тұрақты температура кезінде оның қысымы мен көлемінің көбейтіндісі тұрақты болып қалады.
(10.11). Бұл теңдеуді изотерма теңдеуі деп атайды және ол Бойль-Мариотт заңының математикалық өрнегі болып табылады: газдың берілген массасы үшін тұрақты температура кезінде оның қысымы мен көлемінің көбейтіндісі тұрақты болып қалады.
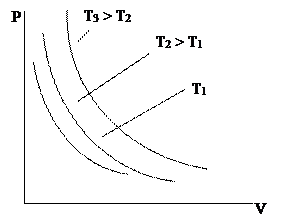 |
| Түрліше температуралар үшін қысымның көлемге тәуелділігі 1. суретте көрсетілген. Изотермалар деп аталатын бұл қисықтар гиперболалар болып табылады. |
Гей Люссак заңы. Енді газдың  қысымы тұрақты болып қалып, оның температурасы мен көлемі өзгеретін болсын. Мұндай шартты орындау үшін газды жылжымалы поршенмен жабылған цилиндрге ұстайық. Мұндай цилиндрдегі газдың температурасын өзгерткен кезде газдың қысымы өзгеріп, ол поршенді жылжытады да, газдың көлемі де өзгереді. Газ тепе-теңдік күйіне келген кезде газ қысымы бастапқы мәнін қабылдайды. (10.10) теңдеуінен көріп отырғандай, мұндай жағдайда газ көлемінің оның температурасына қатынасы өзгеріссіз қалады:
қысымы тұрақты болып қалып, оның температурасы мен көлемі өзгеретін болсын. Мұндай шартты орындау үшін газды жылжымалы поршенмен жабылған цилиндрге ұстайық. Мұндай цилиндрдегі газдың температурасын өзгерткен кезде газдың қысымы өзгеріп, ол поршенді жылжытады да, газдың көлемі де өзгереді. Газ тепе-теңдік күйіне келген кезде газ қысымы бастапқы мәнін қабылдайды. (10.10) теңдеуінен көріп отырғандай, мұндай жағдайда газ көлемінің оның температурасына қатынасы өзгеріссіз қалады: 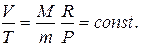
Изобара теңдеуідеп аталатын бұл теңдеу Гей-Люссак заңының математикалық өргені болып табылады; Изобара графигі 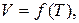 жоғарыдағы өрнектен көріп отырғанымыздай, координаттар басынан шығатын түзу болып табылады.
жоғарыдағы өрнектен көріп отырғанымыздай, координаттар басынан шығатын түзу болып табылады.
Шарль заңы. Егер процесс кезінде газдың көлемі өзгеріссіз қалатын болса, онда газ күйі теңдеуінен 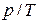 қатынасының өзгеріссіз қалатындығы шығады:
қатынасының өзгеріссіз қалатындығы шығады:
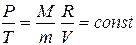 (10.13) Теңдеу Изохора теңдеуі деп аталады және Шарль заңының мазмұны болып табылады.
(10.13) Теңдеу Изохора теңдеуі деп аталады және Шарль заңының мазмұны болып табылады.
Авагадро заңы.Бұл заңды да газ күйінің теңдеуінен шығарып алуға болады: бірдей газ қысымы мен бірдей температура кезінде газдың бірдей көлемдерінде молекулалардың бірдей саны болады.
Түрліше газдардың молекулаларының бірдей санының бірдей температуралары мен бірдей қысым кезінде бірдей көлем қабылдайтындығы шығады. Сондықтан 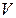 газдың молі берілген қысым мен температура кезінде бірдей көлем қабылдайды. Мысалға,
газдың молі берілген қысым мен температура кезінде бірдей көлем қабылдайды. Мысалға, 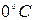 температура және
температура және 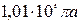 қысым кезінде
қысым кезінде 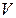 газдың молінің көлемі
газдың молінің көлемі 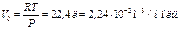 Осындай қалыпты жағдайлар деп аталатын кездерде
Осындай қалыпты жағдайлар деп аталатын кездерде 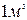 көлемдегі молекулалар саны
көлемдегі молекулалар саны 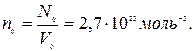 Бұл сан Лошмидт саны деп аталады.
Бұл сан Лошмидт саны деп аталады.
Термодинамикалық жүйе деп өзара және сыртқы ортамен энергия және информациямен алмасулары болатын кез келген денені немесе денелер жиынтығын айтады. Тұйықталған жүйе деп сыртқы ортамен әсерлеспейтін, яғни энергиямен (затпен) де, информациямен де алмаспайтын жүйені айтады. Ашық жүйе деп қоршаған ортамен энергиямен (затпен) де, информациямен де алмасатын жүйені айтады.
Жүйенің күйі көлем 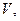 қысым
қысым 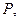 температура
температура 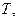 масса
масса 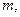 молярлық масса
молярлық масса 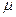 сияқты параметрлермен анықталады. Осы шамаларды байланыстыратын теңдеуді зат күйінің теңдеуі деп атайды. Жалпы түрде күй теңдеуі былай жазылады:
сияқты параметрлермен анықталады. Осы шамаларды байланыстыратын теңдеуді зат күйінің теңдеуі деп атайды. Жалпы түрде күй теңдеуі былай жазылады:
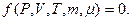 (10.1)
(10.1)
Идеал газ күйін сипаттайтын Менделеев-Клапейрон теңдеуі:
 (10.2)
(10.2)
мұндағы 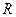
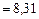
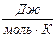 - универсал газ тұрақтысы.
- универсал газ тұрақтысы.
Жүйенің құрамындағы барлық бөлшектердің (молекулалардың немесе атомдардың) кинетикалық және потенциалдық энергияларының қосындысы ішкі энергияны U береді. Ішкі энергия жүйе күйінің функциясы.
Термодинамикалық жүйе сыртқы ортамен екі түрлі (жылу алмасу және жұмыс түрінде) жолмен алмасады. Жылу мөлшері (немесе жылу) деп жылу алмасу процесі кезінде жүйеден (немесе жүйеге) берілген ішкі энергияның бөлігін айтады. Егер жылу сыртқы ортадан жүйеге берілсе, онда жылу оң (Q>0), ал керісінше жағдайда жылу теріс (Q<0) деп есептеледі.
Сыртқы параметрлердің өзгеруі нәтижесінде жүйеден сыртқы ортаға (немесе сыртқы ортадан жүйеге) берілген энергияны жұмыс дейді. Егер энергия жүйеден сыртқы ортаға берілсе, жұмыс оң болады да (А>0), ал керісінше сыртқы ортадан жүйеге берілсе, жұмыс теріс (А<0) болады. Жылу мен жұмыс бір күйден екінші күйге қалай өтетіне тәуелді, сондықтан олар күй функциясы болмай процестің функциясы болады.
Термодинамикалың бірінші заңы.Термодинамикалық жүйеге қатысты энергияның сақталу және айналу заңы термодинамиканың бірінші заңы (бастамасы) деп аталады. Жүйеге берілген жылу мөлшері жүйенің ішкі энергиясын өзгертуге және сыртқы күштерге қарсы жүйенің жұмыс істеуіне жұмсалады:
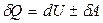 немесе
немесе 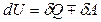 , (10.3)
, (10.3)
мұндағы d таңба жылу мен жұмыс күйдің функциясы емес екендігін, сондықтан олардың толық дифференциалы болмайтындығын көрсетеді. Термодинамиканың бірінші заңы жылу мен жұмыстың арасында эквиваленттік байланыс бар екендігін көрсетеді. 1842 жылы Майер термодинамиканың бірінші заңын тірі организмге қолданып, биоэнергетиканың негізін қалады. Тірі организм ішіндегі тотығу процесі кезінде бөлініп шығатын энергия жылуға және механикалық жұмыс істеуге кетеді.
Идеал газдың жылусыйымдылығы.Массалары әртүрлі және әртүрлі материалды денеге берілген бірдей жылу оларды әртүрлі деңгейде қыздыратындығын тәжірибе көрсетеді. Соған байланысты термодинамикада жылусыйымдылық деген ұғым енгізіледі.
Жылусыйымдылық деп термодинамикалық процесте денеге берілген 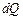 жылудың дененің температурасының өзгеруіне
жылудың дененің температурасының өзгеруіне 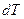 қатынасына тең физикалық шаманы айтады:
қатынасына тең физикалық шаманы айтады:
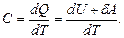 (10.4)
(10.4)
Жүйенің жылусыйымдылығы жүйені қыздыру әдісіне байланысты әр түрлі мәнге ие болады, яғни күйдің функциясы болмай процестің функциясы болады. Жылусыйымдылық дененің химиялық құрамына, массасына, күйіне және термодинамикалық процеске байланысты.
Жылусыйымдылықтың екі түрі болады. Меншікті жылусыйымдылық деп 1 кг затты 1 К-ге қыздыруға қажетті жылу мөлшерін айтады:
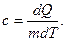 (10.5)
(10.5)
Оның өлшем бірлігі 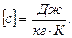
Молярлық жылусыйымдылық деп бір моль затты 1 К-ге қыздыруға қажетті жылу мөлшерін айтады:
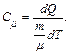 (10.6)
(10.6)
Оның өлшем бірлігі 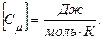 Молярлық жылусыйымдылық молярлық масса мен меншікті жылусыйымдылық көбейтіндісіне тең болады:
Молярлық жылусыйымдылық молярлық масса мен меншікті жылусыйымдылық көбейтіндісіне тең болады:
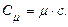 (10.7)
(10.7)
Майер теңдеуі. Термодинамиканың бірінші заңын идеал газда өтетін әр түрлі процестер үшін қарастырайық. Идеал газ деп молекулалар арасында өзара әсерлесу күштері болмайтын, жеке молекулар көлемі ыдыс көлемінен салыстырғанда өте аз және молекулалар арасындағы өзара соқтығысу абсолют серпімді болатын газдарды айтады. Идеал газдың ішкі энергиясы 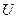 жүйенің құрамындағы барлық бөлшектердің (молекулалардың немесе атомдардың) кинетикалық энергияларының қосындысына тең болады:
жүйенің құрамындағы барлық бөлшектердің (молекулалардың немесе атомдардың) кинетикалық энергияларының қосындысына тең болады:
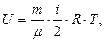 (10.8)
(10.8)
мұндағы 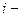 еркіндік дәрежелерінің саны. Ал идеал газдың ішкі энергиясының өзгеруі:
еркіндік дәрежелерінің саны. Ал идеал газдың ішкі энергиясының өзгеруі:
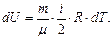 (10.9)
(10.9)
Газдың жұмысының формуласы:
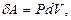 (10.10)
(10.10)
мұндағы 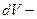 газ көлемінің өзгеруі.
газ көлемінің өзгеруі.
(10.9) және (10.10) пайдаланып термодинамиканың бірінші заңын (10.3) мына түрде жазуға болады:
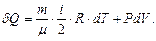 (10.11)
(10.11)
Изохорлық процесс кезінде көлем тұрақты болады (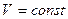 ), газ көлемі өзгермейді, демек
), газ көлемі өзгермейді, демек 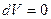 . Сол себептен
. Сол себептен 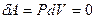 , яғни газда берілетін барлық жылу мөлшері оның ішкі энергиясын өсіруге жұмсалады. Изохорлық процестің молярлық жылусыйымдылығы
, яғни газда берілетін барлық жылу мөлшері оның ішкі энергиясын өсіруге жұмсалады. Изохорлық процестің молярлық жылусыйымдылығы 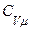 деп белгіленеді. (10.6) формула бойынша
деп белгіленеді. (10.6) формула бойынша 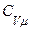 1 моль газ үшін (
1 моль газ үшін ( 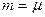 ) (10.9- формуланы ескергенде) былай анықталады:
) (10.9- формуланы ескергенде) былай анықталады:
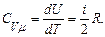 (10.12)
(10.12)
Изобарлық процесскезінде қысым тұрақты болады ( 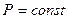 ). Термодинамиканың бірінші заңы:
). Термодинамиканың бірінші заңы: 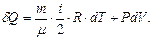 Изобарлық процестің молярлық жылусыйымдылығы
Изобарлық процестің молярлық жылусыйымдылығы 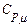 деп белгіленеді. (10.6) формула бойынша
деп белгіленеді. (10.6) формула бойынша 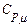 1 моль газ үшін (
1 моль газ үшін ( 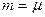 ) былай анықталады:
) былай анықталады:
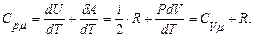 . (10.13)
. (10.13)
Бұл теңдеуді шығарғанда изобарлық процесте идеал газдың істейтін жұмысы
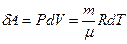 . (10.14)
. (10.14)
екендігін пайдаландық. (10.13) теңдеуі Майер теңдеуі деп аталады. Майер теңдеуі бойынша, 1 моль газдың тұрақты қысымдағы молярлық жылусыйымдылығы тұрақты көлемдегі жылусыйымдылығынан универсал газ тұрақтысына артық болады. Оның себебі изохорлық процеске қарағанда изобарлық процесте газға берілген жылу тек қана ішкі энергияны өзгертіп қоймай жұмыс істеуге де кетеді.
(10.14) формуладан универсал газ тұрақтысының физикалық мағынасы анықталады, демек универсал газ тұрақтысы R бір моль идеал газды тұрақты қысымда 1К қыздырғанда істелетін жұмыстың сан мәніне тең.
(10.13) теңдеуден:
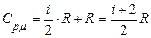 . (10.15)
. (10.15)
Изотермдік процесскезінде температура тұрақты болады (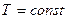 ), газ температурасы өзгермейді, демек
), газ температурасы өзгермейді, демек 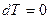 . Сол себептен
. Сол себептен 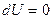 , газдың ішкі энергиясы өзгермейді, яғни газға берілетін барлық жылу мөлшері сыртқы күштерге қарсы жұмыс істеуге кетеді. Жылусыйымдылық шексіздікке ұмтылады.
, газдың ішкі энергиясы өзгермейді, яғни газға берілетін барлық жылу мөлшері сыртқы күштерге қарсы жұмыс істеуге кетеді. Жылусыйымдылық шексіздікке ұмтылады.
Адиабаттық процесс. Пуассон теңдеуі.Сыртқы ортамен жылу алмасусыз жүретін процесті адиабаттық деп атайды. Осы процесс үшін 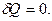 Адиабаттық процесс газдың көлемі тез кеңейген немесе сығылған кезде пайда болады. Адиабаттық процесс үшін термодинамиканың бірінші заңы былай жазылады:
Адиабаттық процесс газдың көлемі тез кеңейген немесе сығылған кезде пайда болады. Адиабаттық процесс үшін термодинамиканың бірінші заңы былай жазылады:
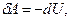 (10.16)
(10.16)
яғни ішкі энергияның кемуі нәтижесінде жүйе жұмыс істейді. Бір моль идеал газ үшін
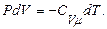 (10.17)
(10.17)
Егер газ адиабаттық кеңейетін болса, онда 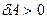 және
және 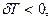 яғни газ суынады. Керісінше газ адиабаттық сығылған кезде
яғни газ суынады. Керісінше газ адиабаттық сығылған кезде 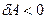 және
және 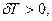 яғни газ қызады.
яғни газ қызады.
Күй теңдеуі (10.2) формула бойынша

Осы теңдеуді (10.17)-ге бөліп (10.13) ескерсек, шығатыны:
1+ 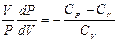 немесе
немесе 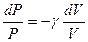 , (10.18)
, (10.18)
мұндағы 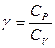 . (10.19)
. (10.19)
(10.18)-ші теңдеуінің шешімі: 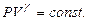 (10.20) Осы формуланы Пуассон теңдеуі деп атайды. (10.12) мен (10.20) формулалардан:
(10.20) Осы формуланы Пуассон теңдеуі деп атайды. (10.12) мен (10.20) формулалардан:
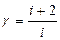 . (10.21)
. (10.21)
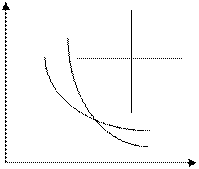 Р
Р
V
10.1- сурет. Изопроцестер графиктері.
1 -изохора, 2- изобара, 3- изотерма,
4- адиабата қисықтары.
Жоғарыда қарастырылған процестердің графиктері 10.1 - суретте көрсетілген.
Дата добавления: 2015-08-08; просмотров: 15111;
