Егер сұйық қабаттары бір-бірінің бетімен сырғанаған тәрізді қозғалса, оны ламинарлық ағын деп аталады.
Егер сұйықтың әрбір нүктедегі жылдамдық векторы орташа мәнінен ретсіз ауытқып отырса, мұндай ағын турбуленттік деп аталады.
Бір ағыннан екіншісіне өту Рейнольдс санымен сипатталады:
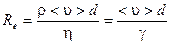
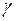 - кинематикалық тұтқырлық, ρ- сұйықтың тығыздығы, <υ> - ағынның орташа жылдамдығы; d - түтіктің диаметрі.
- кинематикалық тұтқырлық, ρ- сұйықтың тығыздығы, <υ> - ағынның орташа жылдамдығы; d - түтіктің диаметрі.
Ламинар ағын үшін Рейнольдс саны (Re≤1000), ламинарлықтан трубуленттікке өту 1000 ≤ Re ≤ 2000, ал Re=2300 ағын турбулентті. Рейнольдс саны өлшемсіз шама, ол сұйықтың тығыздығына және тұтқырлығына байланысты.
Ағыс ламинарлық болсын турбулентік болсын ағыстың 4 маңызды сипаттамалары бар.
- Сұйықты немесе газды сығылатын немесе сығылмайтын деп қарастыруға болады.
- Тұтқырлық немесе ішкі үйкелісі сұйықтың немесе газдың кез-келген қозғалысы кезінде болады, бірақ тұтқырлықты көп жағдайда ескермеуге болады.
- Ағыс тұрақталған немесе стационарлы болуы мүмкін. Мұндай ағыстың жылдамдығы кеңістіктің кез-келген нүктесінде уақыт бойынша тұрақты. Егер ағыс жылдамдығы берілген нүктеде уақыт бойынша өзгеретін болса онда мұндай ағысты стационар емес д.а.
- Ағыс құйынды не құйынсыз болады. Құйынсыз ағыста сұйықтың кез-келген нүктеге қатысты алынған импульс моменті нольге тең болады.
Стокс заңы
Дене тұтқыр ортадан қозғалғанда кедергі пайда болады, оның екі түрлі себебі бар:
1) Дене аққыш формалы жылдамдығы аз болып, құйын пайда болған жағдайда, кедергі күші тек сұйық тұтқыр болған себептен туындайды.
2) Қатты денеге тікелей жанасатын сұйық қабаты оның бетіне жабысады да, толығымен сол денеге ілесе шағын жылдамдықпен қозғалады. Сөйтіп, сұйық қабатының арасында үйкеліс күші пайда болады.
Сұйыққа тасталған денеге үш күш әсер етеді:
1. ауырлық күші: 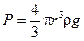 , мұндағы
, мұндағы 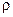 - шардың тығыздығы, r –шардың радиусы;
- шардың тығыздығы, r –шардың радиусы;
2. Архимед күші:  ,
, 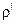 -сұйықтың тығыздығы;
-сұйықтың тығыздығы;
3. кедергі күші: 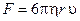 , h -сұйықтың тұтқырлық коэффициенті, v – сұйықтың қозғалыс жылдамдығы.
, h -сұйықтың тұтқырлық коэффициенті, v – сұйықтың қозғалыс жылдамдығы.
Бірқалыпты қозғалыста күштер мына теңдеуге тең: 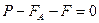
Орындарына қоя отырып, тұтқырлықты тапсақ, мына теңдеу шығады: 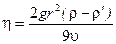
Пуазейль заңы
Бұл әдіс жұқа капиллярдағы сұйықтың ламинар ағысына негізделген, мұндағы тұтқырлық:
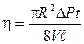
l -капиллярдың ұзындығы, V-капиллярдың көлемі, R –радиусы, DP-сұйықтың қысымы, t – уақыт
Дата добавления: 2015-08-08; просмотров: 3766;
