Позиционные системы счисления. Любое число C в позиционной системе счисления с основанием Р может быть представлено в виде полинома:

Любое число C в позиционной системе счисления с основанием Р может быть представлено в виде полинома:

C= C_n Pⁿ +C_n-1 P^n-1 +…+C₁ P¹ +C₀ P⁰ +C_-1 P^-1 +…+C_-m P^-m ,

или

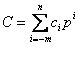
где в качестве C_i могут стоять любые из Р цифр алфавита, а нижние индексы определяют местоположение цифры в числе (разряд):

• положительные значения индексов - для целой части числа (n разрядов);
• отрицательные значения - для дробной (m разрядов).

В вычислительных системах применяются две формы представления чисел:

• естественная форма, или форма с фиксированной запятой (точкой);
• нормальная форма, или форма с плавающей запятой (точкой).

С фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

C = C_n C_n-1 …C₁ C_0, C_-1… C_-m

Запятая опускается, если дробная часть отсутствует. Позиции цифр в такой записи называются разрядами. Разряды нумеруются влево от запятой, начиная с нуля: 0-й,1-й,...(n-1)-й, n-й; и вправо от запятой: 1-й, 2-й,...(m-й).

Значение C_i цифры c_i в позиционных системах счисления определяется номером разряда:

C_i = с_i Рⁱ.

Величина Pⁱ называется весом, или значением, i-го разряда. В позиционных системах счисления значения соседних разрядов отличаются в P раз: левый в P раз больше правого.

Пример 3.1. Десятичная система счисления.

Р=10.

Цифры: 0,1,2,3,4,5,6,7,8,9.

723,19₁₀ =7×10² +2×10¹ +3×10⁰ +1×10^-1 +9×10^-2 .

Пример 3.2. Двоичная система счисления.

Р=2.

Цифры: 0,1.

101110,101₂ = 1×2⁵ +0×2⁴ +1×2³ +1×2² +1×2¹ +0×2⁰ +1×2^-1 +0×2^-2 +1×2^-3

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема в вычислениях.

Максимальное целое число, которое может быть представлено в n разрядах:

N_max = Pⁿ -1.

Минимальное значащее (не равное 0) число, которое можно записать в m разрядах дробной части:

N_min = P^-m .

Имея в целой части числа n, а в дробной части m разрядов, можно записать всего P^n+m разных чисел.

Пример 3.3. Двоичная система счисления.

Р = 2.

n = 10, m = 6.

Возможное для представления значение N лежит в пределах:

0,015<N<1024.

Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных ЭВМ естественная форма представления используется как вспомогательная и только для целых чисел.

С плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, а вторая порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок - целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

,

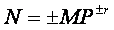где M - мантисса числа (çМç <1);

r - порядок числа (r - целое число);

P - основание системы счисления.

Пример 3.4. Приведем несколько равенств: левая часть равенства – число в естественной форме, правая часть – в нормальной форме. Для записи естественной формы используются 5 разрядов в целой части и 5 разрядов в дробной части.

+00721,35500 = +0,721355×10³; +00000,00328 = +0,328×10^-2;

-10301,20260 = -0,103012026×10⁵.

Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных ЭВМ.

Диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов у порядка и мантиссы) будет

.

Пример 3.5. При Р = 2, n = 10 и m = 6 диапазон чисел простирается примерно от 10^-19 до 10¹⁹. (Сравните примером 3.3).