Стандартные функции. При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа
При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д.
Вычисления часто употребляемых функций осуществляются посредством подпрограмм, называемых стандартными функциями, которые заранее запрограммированы и встроены в транслятор языка.
Таблица стандартных функций школьного алгоритмического языка
| Название и математическое обозначение функции | Указатель функции | ||
| Абсолютная величина (модуль) | | х | | abs(x) | |
| Корень квадратный | 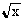
| sqrt(x) | |
| Натуральный логарифм | ln x | ln(x) | |
| Десятичный логарифм | lg x | lg(x) | |
| Экспонента (степень числа е ~ 2.72) | ex | exp(x) | |
| Знак числа x ( - 1, если х<0; 0, если x = 0; 1, если x > 0) | sign x | sign(x) | |
| Целая часть х (т.е. максимальное целое число,не превосходящее х) | int(x) | ||
| Минимум из чисел х и y | min(x,y) | ||
| Максимум из чисел х и y | max(x,y) | ||
| Частное от деления целого х на целое y | div(x,y) | ||
| Остаток от деления целого х на целое y | mod(x,y) | ||
| Случайное число в диапазоне от 0 до х - 1 | rnd(x) | ||
| Синус (угол в радианах) | sin x | sin(x) | |
| Косинус (угол в радианах) | cos x | cos(x) | |
| Тангенс (угол в радианах) | tg x | tg(x) | |
| Котангенс (угол в радианах) | ctg x | ctg(x) | |
| Арксинус (главное значение в радианах) | arcsin x | arcsin(x) | |
| Арккосинус (главное значение в радианах) | arccos x | arccos(x) | |
| Арктангенс (главное значение в радианах) | arctg x | arctg(x) | |
| Арккотангенс (главное значение в радианах) | arcctg x | arcctg(x) | |
В качестве аргументов функций можно использовать константы, переменные и выражения. Например:
| sin ( 3.05 ) min ( a, 5) | sin ( x ) min ( a, b ) | sin ( 2 * y + t / 2 ) min ( a + b , a * b ) | sin((exp(x) + 1) ** 2) min(min(a, b), min(c, d)) |
Каждый язык программирования имеет свой набор стандартных функций.
Дата добавления: 2015-08-08; просмотров: 1296;
