Базовые понятия численных методов

В численных методах функции непрерывного аргумента заменяются функциями целочисленного аргумента – сеточными функциями. Сеточную функцию можно рассматривать как функцию целочисленного аргумента.

y=y(x) y=y(x_i)=y(i)=y_i i=1,2..n

y y

х х₁ х_n

Рис. 5.2

Разностью первого порядка будем называть результат вычитания двух соседних значений y:

Dy_i=y_i+1-y_i (правая разность) (5.4)

Ñy_i=y_i-y_i-1 (левая разность) (5.5)

Предположим, что надо вычислить сумму значений

y_n =x₁+ x₂+…+ x_n= 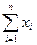. (5.6)

Тогда вычисления организуются следующим образом. Задается начальное значение y₀=0, а затем последовательно, начиная с i=1, находятся числа y_i, связанные реккурентным соотношением

y_i= y_i-1+x_i, i=1, 2, …n. (5.7)

Для вычисления произведения вида

y_n =x₁*x₂*…* x_n= 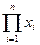(5.8)

достаточно задать начальное значение у₀=1 и воспользоваться реккурентным соотношением

y_i= y_i-1*x_i, i=1, 2, …n. (5.9)

Уравнения (5.7) и (5.9) являются частным случаем линейного разностного уравнения первого порядка:

у_i=q_i*y_i-1+f_i , i=1,2,…n, (5.10)

где q_i, f_i - заданные числа, а у_i – искомые значения.

Для данного уравнения рассматривается задача нахождения всех у_i при заданном значении у₀ . Ясно, что решение этой задачи существует и оно единственно.