Строение атома. 1. Опыт Резерфорда по рассеянию α-частиц на ядрах свидетельствует о том, что в атоме, размер которого ~ 10–8 см
1. Опыт Резерфорда по рассеянию α-частиц на ядрах свидетельствует о том, что в атоме, размер которого ~ 10–8 см, имеется положительно заряженное ядро размером ~ 10–13 см, в котором сосредоточена практически вся его масса.
2. Для объяснения стабильности ядер и линейчатых спектров получения атомов, описываемых обобщенной формулой Бальмера 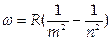 , где m и n — целые числа, при этом n = m + 1, т + 2,..., a R = 2, 07∙1016с–1 постоянная Ридберга, Н. Борсформулировал постулаты:
, где m и n — целые числа, при этом n = m + 1, т + 2,..., a R = 2, 07∙1016с–1 постоянная Ридберга, Н. Борсформулировал постулаты:
1. Электроны движутся вокруг ядра по круговым орбитам, среди которых разрешенными являются некоторые дискретные орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из этих орбит не получает электромагнитных волн. Эти орбиты называются стационарными.
2. Излучение испускается или поглощается в виде кванта энергии hω при переходе из одного стационарного состояния на другое: ħω = Еп – Ет.
3. Условия квантования Бора:
Угловой момент электрона, движущегося по разрешенной орбите rп, должен быть кратна постоянной Планка ħ: L = mevrn = ħn, n = 1,2,3,.... (В дальнейшем будет использоваться система единиц СГСЕ, в которой ko = 1). Из этого условия следует выражение для радиусов разрешенных орбит: 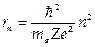 . Для атома водорода (Z = 1) радиус первой орбиты, называемой боровским радиусом равен rо = 0,529.10–8 см.
. Для атома водорода (Z = 1) радиус первой орбиты, называемой боровским радиусом равен rо = 0,529.10–8 см.
Энергия электрона дается выражением: 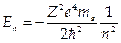 . Поэтому энергия излучаемого фотона, переходящего с орбиты n на орбиту m равна hω = Ет — Еп =
. Поэтому энергия излучаемого фотона, переходящего с орбиты n на орбиту m равна hω = Ет — Еп =  . Энергия электрона атома водорода на первой боровской орбите равна
. Энергия электрона атома водорода на первой боровской орбите равна 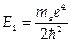 = –2,17∙10–18 Дж = –13,6 эВ Знак минус означает, что электрон находится в связанном состоянии. Для того, чтобы оторвать электрон от атома, ему надо сообщить это количество энергии. Эта энергия называется энергией ионизации.
= –2,17∙10–18 Дж = –13,6 эВ Знак минус означает, что электрон находится в связанном состоянии. Для того, чтобы оторвать электрон от атома, ему надо сообщить это количество энергии. Эта энергия называется энергией ионизации.
4. Уравнение Шредингера
Волновая функция свободно движущееся частицы ψ(x,t) является решением уравнения Шредингера (одномерный случай)
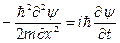 .
.
Если частица движется в поле, характеризующимся потенциальной энергией U, то
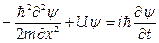 .
.
Если U явно не зависит от энергии, то имеем уравнение Шредингера для стационарных состояний (одномерный случай)
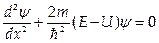 .
.
Дата добавления: 2015-08-08; просмотров: 974;
