Магнитная сила как релятивистское следствие закона Кулона
Подробно разберем следующую несложную задачу.
Вдоль прямолинейного тока I на расстоянии b от него движется со скоростью V точечный заряд q (рис. 14.1.). Какая сила действует на этот заряд?
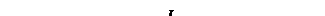
Рис. 14.1.
Вначале рассмотрим эту задачу в лабораторной системе отсчета. Проводник с током не несет избыточных зарядов, следовательно, на заряд q действует только магнитная сила Лоренца (см. 9.11):
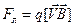 . (14.1)
. (14.1)
Здесь 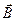 — вектор магнитной индукции поля прямолинейного тока I.
— вектор магнитной индукции поля прямолинейного тока I.
Hа расстоянии b от проводника индукция такого поля равна (см. 8.7):
В = 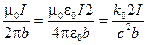 . (14.2)
. (14.2)
Здесь мы воспользовались тем, что 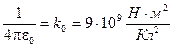 , а
, а
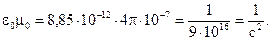
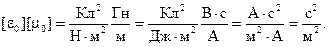
Понятно, что 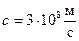 — скорость света в вакууме.
— скорость света в вакууме.
Таким образом, мы установили, что на движущийся заряд будет действовать сила, направленная к проводнику с током. Модуль этой силы равен
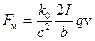 . (14.3)
. (14.3)
Теперь рассмотрим эту же задачу, но в штрихованной системе отсчета, движущейся вместе с зарядом q со скоростью v (рис. 14.2.).

Рис. 14.2.
В этой системе отсчета заряд неподвижен и поэтому магнитная сила отсутствует.
В лабораторной системе отсчета, как уже отмечалось, проводник не имеет избыточного заряда. Это означает, что линейные плотности положительных и отрицательных зарядов в проводнике одинаковы по величине
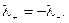
В движущейся системе отсчета расстояния между положительными ионами уменьшатся вследствие лоренцева сокращения, поэтому линейная плотность положительных зарядов возрастет и станет равной
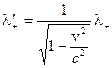 (14.4)
(14.4)
Увеличится и линейная плотность отрицательных зарядов — электронов. При этом необходимо учесть, что в проводнике с током отрицательные заряды участвуют в направленном движении со скоростью vн. Это скорость их движения в неподвижной лабораторной системе отсчета. В движущейся системе отсчета скорость электронов будет выше скорости положительных ионов, поэтому увеличение плотности отрицательных зарядов будет больше, чем положительных.
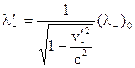 . (14.5)
. (14.5)
Еще раз напомним, что электроны имеют скорость направленного движения vн и в лабораторной системе отсчета, поэтому в этой системе линейная плотность отрицательного заряда равна
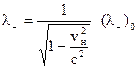 .
.
Отсюда найдем линейную плотность отрицательного заряда в проводнике при отсутствии тока
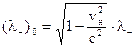 . (14.6)
. (14.6)
Используя этот результат в (14.5), получим
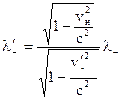 .
.
Ведя следующие обозначения
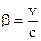 ,
, 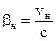 и
и 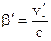 ,
,
перепишем последнее уравнение в таком виде:
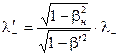 .
.
Воспользуемся теперь релятивистским правилом сложения скоростей:
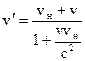 , (14.7)
, (14.7)
или
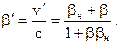
Теперь линейную плотность отрицательных зарядов проводника в движущейся системе отсчета можно представить так:
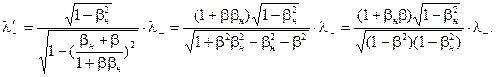
И, наконец, в окончательном виде:
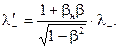 (14.8)
(14.8)
Теперь подсчитаем линейную плотность заряда на проводнике в движущейся системе отсчета. (Это та величина, которая в лабораторной системе равнялась нулю: l = l+ + l– = 0).
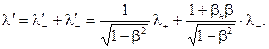
Но 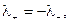 поэтому
поэтому
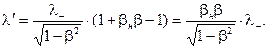
Здесь 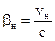 и
и 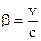 , значит
, значит
 . (14.9)
. (14.9)
Заметим, что плотность отрицательного электрического заряда 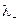 связана с силой электрического тока I. Действительно,
связана с силой электрического тока I. Действительно,
I = j S = –e vнnе S = – 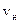
 .
.
Здесь j = 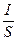 — плотность тока,
— плотность тока,
enеS = 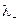 — линейная плотность отрицательного заряда на проводнике.
— линейная плотность отрицательного заряда на проводнике.
Отсюда следует, что 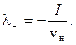
Таким образом, линейная плотность заряда на проводнике в движущейся системе отсчета отлична от нуля и равна (см. 14.9)
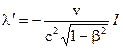 .
.
Проводник с такой плотностью заряда создает электростатическое поле, напряженность которого на расстоянии b от проводника равна (см. 2.13)
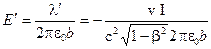 .
.
В таком электрическом поле на неподвижный заряд будет действовать сила
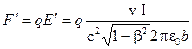 . (14.10)
. (14.10)
Согласно теории относительности, для наблюдателя в неподвижной системе отсчета эта сила будет равна
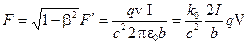 . (14.11)
. (14.11)
Эта электрическая сила совпадает с той магнитной силой, которая была получена нами ранее (см. 14.3). Таким образом, к «магнитной» силе можно прийти, воспользовавшись только законом Кулона и известными положениями теории относительности.
Подвод итог, модно сделать вывод, что F и F’ — одна и та же сила, только в лабораторной системе отсчета она «магнитная», а в системе отсчета, в которой заряд q неподвижен, — она «электрическая».
Можно, конечно, создать и такую систему отсчета, в которой одновременно будут присутствовать обе эти составляющие
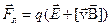 .
.
Дата добавления: 2015-08-08; просмотров: 1049;
