Пример 2. В первом примере электрическое поле создавал заряженный проводник, поэтому в лабораторной системе отсчета магнитное поле отсутствовало .

В первом примере электрическое поле создавал заряженный проводник, поэтому в лабораторной системе отсчета магнитное поле отсутствовало .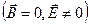

Теперь рассмотрим иную ситуацию: магнитное поле создается прямолинейным проводником с током I. В лабораторной системе отсчета проводник электронейтрален, поэтому электрическое поле отсутствует .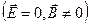

Вновь оценим поля, возникающие в системе 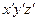, движущейся вдоль проводника со скоростью 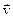(рис. 14.5).

Рис. 14.5.

На пробный положительный заряд q, неподвижный в штрихованной системе, будет действовать только электрическая сила (14.10) :

.

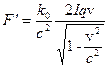Это означает, что в движущейся системе отсчета существует электрическое поле, напряженность которого равна

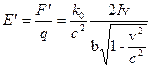. (14.17)

Этот вектор направлен к проводнику, так как вследствие лоренцева сокращения на проводнике появляется избыточный отрицательный заряд.

Ток в проводнике будет определяться движением в штрихованной системе отсчета как отрицательных носителей заряда со скоростью 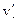, так и положительных .

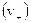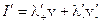. (14.18)

Здесь 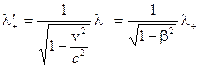— линейная плотность положительных зарядов на проводнике (см. 14.4),

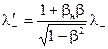— линейная плотность отрицательных зарядов на проводнике (см. 14.7),

v — скорость ионов,

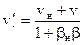— скорость направленного движения электронов в движущейся системе отсчета 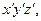(см. 14.7).

Учитывая, что 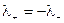, ток в движущейся системе отсчета (14.18) представим в следующем виде:

.

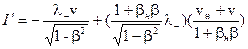Произведя несложные преобразования этого выражения, получим:

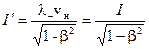. (14.19)

Именно этот ток 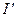и определит индукцию магнитного поля в движущейся системе отсчета (14.13)

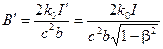. (14.20)

Этот вектор, согласно правилу буравчика, направлен перпендикулярно плоскости рисунка (рис. 14.6.).

Рис. 14.6.

Сопоставляя результаты (14.17) и (14.20), вновь найдем связь магнитного и электрического полей в движущейся системе отсчета. В векторном виде она может быть представлена так:

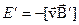. (14.21)

Считая, что результат не изменится, если проводник с током будет двигаться со скоростью 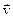в лабораторной системе отсчета, последнему соотношению можно придать следующий вид

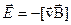. (14.22)

Полученные результаты — (14.16) и (14.22) — означают, что электрическое и магнитное поля представляют собой части единого электромагнитного поля, структура которого определяется выбором системы отсчета.

Рекомендуемая литература

Савельев И.В. Курс физики. Т. 2. — СПб МИФРИЛ, М.: Наука, 1996.

Калашников С.Г. Электричество. М.: Наука, 1985.

Орир Дж. Физика. Т. 1. — М.: Мир, 1988.

Парселл Э. Берклеевский курс физики, Т. II, Электричество и магнетизм. — М.: Наука, 1975.

Содержание

Лекция 1 «Основы электростатики». 2

1. Введение. Предмет классической электродинамики. 2

1.1. Из истории электродинамики. 2

1.2. Электродинамика и научно-технический прогресс. 3

1.3. Свойства электрических зарядов. 4

1.4. Закон Кулона. 4

2. Электрическое поле. 5

2.1. Идеи близко - и дальнодействия. 5

2.2. Напряжённость электрического поля. Поле точечного заряда. Графическое представление электрических полей. 5

3. Принцип суперпозиции электрических полей. 8

3.1. Поле диполя. 9

3.2. Поле бесконечно заряженной нити. 10

Лекция 2 «Теорема Гаусса для электрического поля». 12

1. Поток вектора напряжённости электрического поля. 12

2. Теорема Гаусса для электрического поля. 14

3. Применение теоремы Гаусса для расчёта электрических полей. 16

3.1. Поле бесконечной заряженной нити. 16

3.2. Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора 18

3.3. Поле сферического конденсатора. 20

Лекция 3 «Потенциал электростатического поля». 22

3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов. 22

3.2. Теорема о циркуляции в вектора напряжённости электростатического поля. 26

3.3. Связь напряжённости и потенциала электростатического поля. 27

3.4. Примеры расчёта потенциала электростатических полей. 29

3.4.1. Потенциал поля точечного заряда. 29

3.4.2. Разность потенциалов на обкладках сферического конденсатора. 29

Лекция 4 «Электростатика проводников». 31

1. Электрическое поле заряженного проводника. 31

2. Проводники во внешнем электрическом поле. Явление электростатической индукции. Электрическая защита. 34

3. Электроёмкость проводника. Конденсаторы. Емкость конденсаторов. 35

3.1. Ёмкость плоского конденсатора. 37

3.2. Ёмкость сферического конденсатора. 37

3.3. Ёмкость цилиндрического конденсатора. 38

4. Энергия электрического поля. Плотность энергии. 39

Лекция 5 «Электрическое поле в диэлектриках». 42

1. Типы диэлектриков. Поляризация диэлектриков. Поляризуемость и вектор поляризации. 42

2. Диэлектрическая проницаемость. Вектор электрического смещения. 45

3. Законы электрического поля в диэлектриках. 47

3.1. Закон Кулона. 47

3.2. Теорема Остроградского-Гаусса. 48

4. Условия на границе двух диэлектриков. 49

Лекция 6 «Постоянный электрический ток». 52

1. Электрический ток. Характеристики электрического тока. 52

2. Законы Ома для участка цепи. 54

2.1. Закон Ома в интегральной форме. 54

2.2. Закон Ома в дифференциальной форме. 56

3. Пример расчёта силы тока в проводящей среде. 57

4. Закон Джоуля-Ленца в интегральной и дифференциальной формах. 58

Лекция 7 «Постоянный электрический ток». 60

1. Сторонние силы. Источники тока. Э.д.с. источника. 60

2. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура. 61

3. Правила Кирхгофа. 63

4. Классическая теория электропроводности металлов. 66

Лекция 8 «Электромагнетизм. Основы магнитостатики». 68

1. Электростатика. Краткий обзор. 68

2. Магнитное взаимодействие электрических токов. 69

3. Магнитное поле. Закон Ампера. Индукция магнитного поля. 70

4. Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа. 72

4.1. Магнитное поле прямолинейного тока. 73

4.2. Магнитное поле на оси кругового тока. 75

4.3. Магнитное поле движущегося заряда. 76

Лекция 9 «Основы магнитостатики». 78

1. Краткий обзор предыдущей лекции. 78

2. Сила Лоренца. 80

3. Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики. 81

4. Примеры расчёта магнитных полей. 87

4.1. Поле прямолинейного тока. 87

4.2. Поле бесконечного соленоида. 88

4.3. Поле тороида. 89

Лекция 10 «Электромагнитная индукция. Энергия магнитного поля». 90

1. Явление электромагнитной индукции. 90

1.1. Опыты Фарадея. 90

1.2. Правило Ленца. 92

2. Электродвижущая сила индукции. Закон Фарадея. 93

3. Индуктивность. Индуктивность соленоида. Явление самоиндукции. 97

4. Токи размыкания и замыкания цепи. Энергия и плотность энергии магнитного поля. 98

Лекция 11 «Электрические колебания». 102

1. Колебательные контуры. Квазистационарные токи. 102

2. Собственные электрические колебания. 104

2.1. Собственные незатухающие колебания. 104

2.2. Собственные затухающие колебания. 105

3. Вынужденные колебания. 108

3.1. Резистор (R) в цепи переменного тока. 108

3.2. Ёмкость в цепи переменного тока I = I₀coswt 109

3.3. Индуктивность в цепи переменного тока. 109

3.4. Вынужденные колебания. Резонанс. 109

3.5. Проблема косинуса фи. 113

Лекция 12 «Теория Максвелла». 114

1. Две трактовки явления электромагнитной индукции.
Вихревое электрическое поле. 114

2. Ток смещения. Обобщение теоремы о циркуляции магнитного поля. 116

3. Полная система уравнений Максвелла и их физический смысл. 118

Лекция 13 «Электромагнитные волны». 119

1. Волновой процесс. Уравнение плоской волны. Волновое уравнение. 119

2. Плоская электромагнитная волна. Свойства электромагнитных волн. 121

3. Энергия электромагнитных волн. Плотность потока энергии.
Вектор Пойнтинга. 124

4. Примеры вычисления плотности потока энергии. 125

4.1. Плотность потока энергии в плоской электромагнитной волне в вакууме. 125

4.2. Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике. 126

Лекция 14 «Магнетизм как релятивистский эффект». 127

1. Магнитная сила как релятивистское следствие закона Кулона. 127

2. Релятивистское преобразование магнитных и электрических полей. 130

2.1. Пример 1. 131

2.2. Пример 2. 132

Рекомендуемая литература. 134

Содержание. 135