Мкость цилиндрического конденсатора

Сообщим обкладкам цилиндрического конденсатора заряды (+q) и (–q) (рис. 4.11.). Вычислим напряжённость поля между обкладками. Для этого выберем гауссову замкнутую поверхность в виде цилиндра радиусом R₁ < r < R₂ и высотой l. Пренебрегая краевыми эффектами (!), запишем уравнение теоремы Гаусса

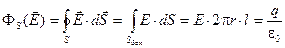
Рис. 4.11.

Из последнего равенства заключаем, что

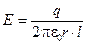(4.9)

Теперь, воспользовавшись связью напряжённости и потенциала электрического поля 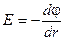, вычислим разность потенциалов между обкладками цилиндрического конденсатора

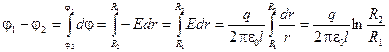
Как и в случае других конденсаторов, разность потенциалов на обкладках цилиндрического конденсатора оказалась пропорциональной заряду q. Поэтому ёмкость конкретного цилиндрического конденсатора оказывается величиной постоянной, зависящей только от размеров этого конденсатора

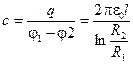(4.10)