Мкость сферического конденсатора

Обкладками такого конденсатора являются две концентрические сферы радиусами R₁ и R₂ (рис. 4.10, b).

На прошлой лекции была вычислена разность потенциалов между обкладками сферического конденсатора. Она оказалась пропорциональна заряду конденсатора (см. 3.27).

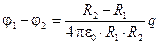
Ёмкость, равная по определению отношению заряда к разности потенциалов, для сферического конденсатора, составит следующую величину

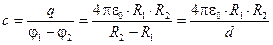(4.8)

Этот результат свидетельствует о том, что ёмкость сферического конденсатора зависит от размеров сфер (R₁ и R₂) и от величины зазора d (d = R₁ – R₂) между ними.

Интересно, что при достаточно малом зазоре d, когда R₁ » R₂ = R, можно записать ёмкость сферического конденсатора так:

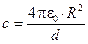
Но 4pR² = S — площадь поверхности сферы. Поэтому

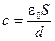
и ёмкость сферического конденсатора оказывается равной ёмкости «эквивалентного» плоского конденсатора.