Теорема Штейнера. В механике твердое тело обычно рассматривают как механическую систему, масса т которой непрерывно распределена по объему V тела

В механике твердое тело обычно рассматривают как механическую систему, масса т которой непрерывно распределена по объему V тела, так что при вычислении момента инерции тела, суммирование в формуле (8), переходит в интегрирование

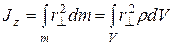, (10)

где 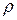– плотность тела, 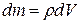– масса малого элемента объема dV, отстоящего от оси вращения тела на расстоянии .

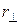Пример:

Расчет момента инерции однородного цилиндра относительно его геометрической оси Z.

Мысленно разделим цилиндр высоты h и радиуса R на концентрические слои толщиной dr. Если плотность материала цилиндра 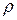, то масса dm , заключенная в слое dr; будет равна: 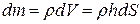; так как 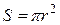, , 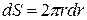то .

Используя формулу (10), находим момент инерции однородного цилиндра:

,

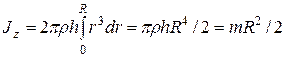где 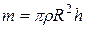– масса цилиндра.

Подсчет момента инерции тела относительно произвольной оси облегчается, если воспользоваться теоремой Штейнера:

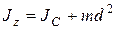, (11)

где 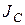– момент инерции тела относительно оси, проходящей через центр масс тела и параллельной оси Z; d – расстояние между осями.