МОЛЕКУЛАЛЫҚ ФИЗИКА НЕГІЗДЕРІ
1. Зерттеудің термодинамикалық және статистикалық әдістері.Денелердің қасиеті мен құрылысының, оны құрайтын бөлшектердің өзара әсерінің және олардың қозғалыс сипатының олардың агрегат күйіне тәуелділігін қарастыратын физика бөлімі-молекулалық физика деп аталады.
Кез келген денедегі атомдар (молекулалар) саны өте көп мөлшерде болады. Мысалы, кәдімгі қысым мен температурада 1м3 газ құрамында 1025 шамасындай молекула, ал қатты денелер мен сұйықтарда–1029 шамасында молекула болады. Егер әрбір атомның (молекуланың) қозғалысы классикалық механика заңына бағынады десек, онда осындай көптеген молекулалардың қозғалысының дифференциалдық теңдеулер жүйесін жазу мүмкін емес болар еді. Жазған күнде де теңдеулердің шешуін жазу мүмкін емес. Сондықтан да, дененің бір молекуласының (немесе атомының) қозға-лысын сипаттау, мысалы оның траекториясын, орын ауыстыруы мен жылдамдығын классикалық механиканың әдістерімен түсіндіру мүмкін болмайды, олар уақыт бойынша кездейсоқ түрде өзгереді.
Өте көп бөлшектен тұратын макроскопиялық жүйенің физикалық қасиеті бірін-бірі толықтырып отыратын статистикалық және термо-динамикалық деп аталатын екі әдіспен зерттеледі. Статистикалық әдіс ықтималдылық теориясын және зерттелетін жүйенің құрылысын белгілі бір моделіне қолдануға негізделген. Мысалы, газдарда молекулалардың темпе-ратурамен байланысты жылулық қозғалысының орташа жылдамдығының мәндерін және олардың энергияларын анықтауға болады. Сондай ақ, қатты денелерде бөлшектердің тербелмелі қозғалысының орташа энергиясының температурадан тәуелділігін анықтауға болады. Макроскопиялық жүйелер-дің физикалық қасиеттерін статистикалық әдіс көмегімен зерттейтін теория-лық физика бөлімі статистикалық физика деп аталады.
Температура-тек термодинамикада ғана емес, толығымен физикада маңызды роль атқаратын негізгі ұғымдардың бірі. Температура–макроско-пиялық жүйенің термодинамикалық тепе теңдік күйін сипаттайтын физикалық шама. Қазіргі уақытта екі температуралық шкала қолданылады: термодинамикалық және Халықаралық практикалық.
Халықаралық практикалық шкалада қысым 1,013·105 Па болғанда судың қату және қайнау температуралары тиісінше 0 және 1000С (реперлік нүктелер) болады, температура Цельсиймен өлшенеді.
Термодинамикалық температуралық шкалада температура Кельвинмен өлшенеді. Термодинамикалық температура және Халықаралық практикалық шкала бойынша алынған температура Т=273,15+t қатынасымен байланысқан.
Бірлік массаның көлемі меншікті көлем деп аталады. Дене біртекті, яғни тығыздығы r=const болғанда, оның меншікті көлемі u=V/m=1/r тең болады. Тұрақты массада меншікті көлем жалпы көлемге пропорционал болады, онда біртекті дененің макроскопиялық қасиеттерін дене көлемімен сипаттауға болады.
Жүйе күйінің параметрлері өзгере алады. Термодинамикалық параметр-лерінің біреуінің өзгеруімен байланысты термодинамикалық жүйенің кез келген өзгерісі термодинамикалық процесс деп аталады. Егер макроскопия-лық жүйе күйі уақыт өтуіне байланысты өзгермесе, онда ол жүйе термоди-намикалық тепе теңдікте болады.
Қысым дегеніміз сұйық немесе газдың тарапынан бірлік ауданға әсер ететін қалыпты күшке тең шама. Халықаралық бірліктер жүйесінде қысым-ның өлшем бірлігі–Паскаль.
Жүйенің кез келген термодинамикалық параметрін тәуелсіз айнымалы деп қабылданған параметрлермен байланыстыратын теңдеуді күй теңдеуі деп атайды. Біртекті дене үшін қысымды, көлемді және температураны байланыстыратын күй теңдеуі газ күйінің термиялық теңдеуі деп аталады.
f (P,V,T) = 0 (7.1)
2. Идеал газдардың молекула-кинетикалық теориясы.Термиялық теңдеуді қолданудың қарапайым объектісі идеал газ болып табылады.
Идеал газды молекула-кинетикалық теория тұрғысынан түсіндіретін болсақ,
1) газ молекулаларының меншікті көлемі газ тұрған ыдыс көлемімен салыстырғанда өте аз;
2) газ молекулалары арасында өзара байланыс күші болмайды;
3) газ молекулаларының өзара және ыдыс қабырғаларымен соқтығысуы серпімді болады.
Молекула–кинетикалық теория заттың ең қарапайым газ түріндегі күйін түсіндіре алады.
Газды бір–бірінен барынша салыстырмалы алыс орналасқан молекула-лардың жиынтығы деп есептеуге болады. Молекулалар бір–бірімен немесе газ тұрған ыдыстың қабырғаларымен соқтығысқанға дейінгі аралықта еркін жүріп ретсіз қозғалады. Молекулалардың өзара әсер күші соншама аз, оны ескермесе де болады. Газда еркін және ретсіз қозғалып жүргетін серпімді молекуланы шарлар тобы деп қарастырады. Молекулалардың мөлшері өте кішкентай, сондықтан да олардың қорытқы көлемін ыдыстың көлемімен салыстырғанда ескермеуге болады. Молекулалар жылдамдықтарының шамалары да әртүрлі болады. Соқтығысудың әсерінен жылдамдықтың өсуі немесе азаюы мүмкін.
Сонымен, газды еркін қозғалып жүретін бөлшектердің жиыны ретінде қарастырып, газдардың өздері алып тұрған көлемге тегіс таралу қасиетін және сондай–ақ бір–бірімен араласа алу қасиетін тікелей түсіндіруге мүмкіндік бар.
Молекула–кинетикалық теорияның негізгі теңдеуі газ күйін сипаттай-тын параметрлер мен молекулалар қозғалысын байланыстырады, яғни газ қысымы мен көлемінің тәуелділігін және молекулалардың ілгерілемелі еркін қозғалысының кинетикалық энергиясының арасындағы байланысты қарастырады. Газға түсірілген қысымды F/S=Р десек және бірлік көлемдегі молекулалар саны n/V=n0 болатынын ескерсек, онда p=1/3n0 mc2 болады.
Газдың ыдыс қабырғаларына түсіретін қысымы көлем бірлігіндегі молекулалардың санымен, молекулалардың массасымен және олардың жылдамдықтар квадратының орташа мәндерімен анықталатынын ескеріп, соңғы формуланың оң жағын екіге көбейтіп және бөлсек, келесі теңдікті аламыз: p=(2/3)n0(mc2)/2 (7.2)
Мұндағы (mc2)/2=v -бір молекуланың ілгерілемелі қозғалысының орташа кинетикалық энергиясы, сондықтан p=(2/3)n0v (7.3)
Осы формула газдардың кинетикалық теориясының негізгі теңдеуі деп аталады.
Егер dN жылдамдықтары dv интервалында жататын молекулалардың саны болса, онда таралу функциясы деп жылдамдықтары vжәне v+dvаралықтарында жататын молекулалардың dN/N салыстырмалы санын айтады: f(v)dv=dN/N, f(v)=dN/Ndv(7.4)
Мұндағы N-газ молекулаларының саны. Ықтималдықтар теориясын пайдаланып Максвелл таралу функциясын есептеп шығарған:
f(v)=4p (m/2pkT)3/2 e –mv 2/ ( 2kT) v2 (7.5)
Функция нольден басталып максимумға жетіп, содан асимтоталық түрде нольге ұмтылады (13-сурет). Таралу функциясы газдың тегіне (молекуланың массасына), vжылдамдыққа сәйкес келетін молекуланың mv2/2 кинетикалық энергиясына және күй параметрі Т-ға тәуелді, оның максимал мәніне сәйкес келетін жылдамдығын ең ықтимал жылдамдық деп атайды. (7.1)-теңдеуді v бойынша дифференциалдап, табылған өрнекті нольге теңестіріп ең ықтимал жылдамдықты табамыз:
vықт= Ö2kT/m =Ö 2RT/m (7.6)
Бұдан таралу функциясының максимумы температура артқанда (немесе молекуланың массасы кемігенде) оңға қарай жылжиды және төмендейді, бірақ қисықтық қамтитын ауданы өзгеріссіз қалады (14-сурет).
 f
f
f Т1< T2
dS=dN/N
v v
vықт vортv2 dv
13-сурет 14-сурет
Молекулалардың ілгерілемелі қозғалысының орташа арифметикалық жылдамдығы мынаған тең:
¥ ¥
vорт=ò vf(v)dv=(m/2pkT)3/24pò e–mv 2/( 2kT)v2dv=Ö 8kT/p m (7.7)
0 0
Осыған ұқсас жылдамдық квадратының орташа мәні үшін төмендегі өрнекті аламыз: ¥ ¥
v2орт=òv2f(v)dv=(m/2pkT)3/24pòe–mv 2/( 2kT)v4dv=3RT/m (7.8)
0 0
Орташа квадраттық жылдамдық деп мына шаманы айтады:
v2орт=Ö v2орт=Ö 3kT/ m=Ö 3RT/ m=1.22vықт (7.9)
Максвелл тағайындаған молекулалардың жылдамдықтар бойынша таралу заңы кез келген N саны үшін, тек тепе-теңдікте тұрған, күш өрісі жоқ жағдайдағы газ үшін ғана орындалады. v=Ö2Ek/m және dv=1/Ö2Ekm шамаларына алмастыру жасап молекулалардың ілгерілемелі қозғалысының кинетикалық энергияларының мәндері бойынша таралу заңын табуға болады:
f(Eорт)=(2/Öp)(kT)-3/2E2/1ортe-Ek/kT (7.10)
Тұрақты Т температурада газдың Р қысымының h биіктігінің артуына қарай экспоненциал түрде кему заңы барометрлік формуламен беріледі:
Ph=P0 e-Mgh/kT (7.11)
P қысымын nkT арқылы, ал M/R–ді m/k-мен алмастырып, кез келген күштің потенциал өрісінде бөлшектердің биіктік бойынша, сонымен қатар олардың потенциалдық энергияларының мәндері бойынша таралу заңын (Больцманның таралу заңын) анықтаймыз:
n=n0 e-Mgh/RT = n0 e-mgh/RT = n0 e- E /kT (7.12)
мұндағы n0–биіктігі нольге тең бірлік көлемдегі бөлшектер саны, ал n-h биіктіктегі дәл сондай сан. (7.4) формуладан потенциалдық энергиясы аз болатын жерлерде бөлшектердің тығыз орналасып, ал потенциалдық энергиясы көп болатын жерлерде сирегірек орналасатындығы шығады.
Т=const болғанда молекулалардың еркін жолының ұзындығы қысымға кері пропорционал болатынын көреміз.
Газ тепе-теңдік күйде болғанда оның температурасы мен қысымы көлемнің кез-келген нүктесінде тұрақты болады.
3. Тасымалдау құбылысы.Тепе-теңдік бұзылса да, молекулалардың қозғалысы нәтижесінде біраз уақыттан кейін ол қайта орнына келеді. Осылайша газ молекулалары бір жерден екінші жерге көшіп жүреді. Бұл диффузия құбылысы арқылы түсіндіріледі. Бұл тұста газ температурасы артты делік.
Температурасы жоғары молекуланың кинетикалық энергиясы да көп болады, ол тез қозғалып орын ауыстырып, басқа молекулаларға жылу береді. Бұл жылу өткізгіштік арқылы жүзеге асады.
Егер газдың екі қабаты бір-біріне қарағанда әртүрлі жылдамдықпен қозғалатын болса, онда олардың арасында ішкі үйкеліс пайда болады. Ішкі үйкеліс нәтижесінде жылдамдығы артық қабаттың жылдамдығы азайып, жылдамдығы аз қабаттың жылдамдығы артады. Соңында жылдамдықтар теңеседі.
Диффузия, жылу өткізгіштік және iшкі үйкеліс процестеріне ортақ қасиет сол, олар молекулалардың бір орнынан екінші орынға ауысуы кезінде, яғни молекула тасымалдау кезінде пайда болады.
Диффузия кезінде масса, жылу өткізгіштік кезінде энергия, iшкі үйкеліс кезінде импульс тасымалданады. Яғни оларды тасымалдау құбылысы арқылы түсіндіруге болады.
Тасмалдаудың жалпы теңдеуін қортып шығару үшін қыры l-ге тең куб аламыз. Осы кубтың ауданы DS болатын бір жағы ОХ осіне перпендикуляр орналассын. Сонда барлық молекулалардың 1/6 бөлігі осы ауданшаға қарай бағытталып қозғалса, 1/6 бөлігі оған қарсы қозғалады. Сонда Dt уақыт ішінде DS арқылы мынандай молекула өтеді:
n =(1/6) n0 DS l =(1/6) n0 DSvDt (7.13)
мұндағы n0-бірлік көлемдегі молекулалар саны, v-молекула жылдамдығы.
Молекулалар DS ауданшасы арқылы белгілі бір физикалық шаманы (j) тасымалдайды, яғни nj=(1/6)(n0 j) vDSDt (7.14)
Газ толтырылған көлемнің әр тұсындағы молекулалар саны түрліше болады. Сонда әр тұстағы nj физикалық шаманың мөлшері де әр алуан болады. Айталық, х1–нүктесінде ол шама (n0j)1–ге, х2–нүктесінде ол шама (n0 j)2 –ге тең болсын. Немесе (n0j)1 > (n0j)2, сонда физикалық шама х1–ден X2 нүктесіне қарай тасымалданады. Осы екі нүктедегі физикалық шама үшін былай жазуға болады:
(nj)1=(1/6)(n0 j)1vортDSDt , (nj)2=(1/6) (n0 j)2vорт DSDt
Бұлардың айырмасы:
D(nj)1=(nj)1-(nj)2=(1/6)(n0j)1vортDSDt–(1/6)(n0j)2vортDSDt=(1/6)vортDSDt[(nj)1–(nj)2]
Сонымен D(nj)1=(1/6)vортDSDt[(nj)1-(nj)2] (7.15)
Енді DS ауданшаның оң және сол жағындағы X1 және X2 нүктелері ол ауданшадан қандай қашықтықта орналасуы керек екенін анықтаймыз. Физикалық шама (j) және бірлік көлемдегі молекулалар санын (n0) өзгерту үшін молекулалар бір-бірімен соқтығысуы қажет. Біз білетін ол қашықтық l-ға тең. n0j шамасының мәні ауданшаның оң және сол жағында l қашықтықта өзгермейді. Олай болса, осы қашықтықтағы n0j шамасының мәнін аламыз. Соңғы өрнектің оң жағын 2lорт-ға көбейтіп және бөлеміз. Сонда D(nj)=(1/6)vортDSDt[((n0j)1-(n0j)2)/2l]2l., 2lорт=Dх екенін ескерсек ,
D(nj)=(1/3)vортlортDSDt[((n0j)1-(n0j)2)/Dх)]=(1/3)vортlорт(D(n0j)/Dх)DSDt (7.16)
Соныменен (nj)=(1/3)vортlорт(D(n0j)/Dх)DSDt (7.17)
Бұл тасымалдаудың жалпы теңдеуі болып табылады.
1.Диффузия. Диффузия кезінде масса тасымалданады, олай болса j=m:
D (n0j)=D(n0 m)=Dr; D(nj)=D(nm)=DM; (7.18)
Осы белгілеулерді тасымалдаудың негізгі теңдеуіне қойсақ:
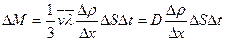 немесе
немесе 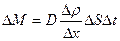 (7.19)
(7.19)
Бұл диффузия теңдеуі немесе Фик заңы деп аталады. Мұндағы 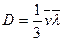 - диффузия коэффициенті, Dr/Dх- тығыздық градиенті.
- диффузия коэффициенті, Dr/Dх- тығыздық градиенті.
Фик заңы: диффузия процесі кезінде оське перпендикуляр орналасқан DS ауданшасы арқылы тасымалданатын масса тығыздық өзгеруіне (градиентіне), ауданшаға (DS) және уақытқа (Dt) тура пропорционал болады.
2. Ішкі үйкеліс. Ішкі үйкеліс кезінде импульс тасымалданады, яғни j=mv.
Сонда D(n0j)=D(n0 mv)=n0 mv=rDv; D(nj)=D(nmv)=DK; (7.20)
Екінші жағынан импульстің өзгеруі күш импульсінің өзгерісіне тең. DK=FDt
Сонда D(nj)=FDt белгілеуін пайдалансақ, тасымалдаудың негізгі теңдеуі былай жазылады: FDt=h(Dv/Dx)DSDt - ішкі үйкеліс үшін Ньютон теңдеуі, мұндағы 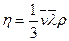 -ішкі үйкеліс коэффициенті, немесе динамикалық тұтқырлық деп аталады. Dv/Dx-жылдамдық градиенті. Ағылшын физигі О.Рейнольдс ағыс сипаты Рейнольдс саны деп аталатын өлшемсіз санмен анықталатынын тағайындады: Rе=r<v>d/h=<v>d/n, мұндағы n=h/r-кинематикалық тұтқырлықдеп аталады.
-ішкі үйкеліс коэффициенті, немесе динамикалық тұтқырлық деп аталады. Dv/Dx-жылдамдық градиенті. Ағылшын физигі О.Рейнольдс ағыс сипаты Рейнольдс саны деп аталатын өлшемсіз санмен анықталатынын тағайындады: Rе=r<v>d/h=<v>d/n, мұндағы n=h/r-кинематикалық тұтқырлықдеп аталады.
3. Жылу өткізгіштік.Бұл процесс кезінде ішкі энергия тасымалданады,
яғни j=(i/2)kT; D(n0j)=D (n0 ikT/2)=ikn0T/2; D(nj)=Dn0ikT/2)=DQ (7.21)
Осыларды тасымалдаудың негізгі теңдеуіне қойсақ: DQ=l(DT/Dx) DSDt,
бұл теңдеу Фурье заңы деп аталады, мұндағы 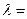
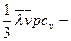 жылу өткізгіштік коэффициенті деп аталады. Фурье заңы: (DS) ауданшасы арқылы (Dt) уақыт ішінде тасымалданатын (DQ) жылу темпера-тураның градиентіне DT/Dx, ауданшаға және уақытқа тура пропорционал болады.
жылу өткізгіштік коэффициенті деп аталады. Фурье заңы: (DS) ауданшасы арқылы (Dt) уақыт ішінде тасымалданатын (DQ) жылу темпера-тураның градиентіне DT/Dx, ауданшаға және уақытқа тура пропорционал болады.
Тасымалдау құбылысын мына кестеден байқауға болады.
| Тасымалдау құбылысы | Тасымалданатын шама | Тасымалдау теңдеуі | Коэффициенті |
| 1. Дифузия | масса | 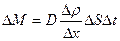
| D= 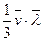
|
| 2. Ішкі үйкеліс | импульс | 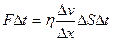
| 
|
| 3.Жылу өткізгіштік | ішкі энергия | 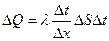
| 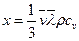
|
Дата добавления: 2015-08-08; просмотров: 4260;
