Термодинамиканың бірінші бастамасын изопроцестерге қолдану.

Газдың күйін сипаттайтын үш параметрдің (р,V,Т) біреуі тұрақты болып отырса, онда мұндай процестерді изопроцестер деп атайды.

1. Изохоралық процесс.Газдың көлемі тұрақты, яғни V=Const болады, сонда dV=0, олай болса газ сыртқы күштерге қарсы жұмыс жасамайды:

d A = ₁ò ² pdV =0

р р

2 1 2

р₁

А

V V₁ V₂ V

15 - сурет 16 – сурет

Осы процестің диаграммасын (15-сурет) салатын болсақ, 1-2 газдың изохо-ралық қыздыру процесін, ал 1-3 газдың изохоралық суыну процесін көрсе-теді. Изохоралық процес кезінде газ жұмыс жасамайды дедік, яғни d A=0.

Ендеше, жоғарыда айтылғандай, изохоралық процес үшін газға берілген барлық жылу оның ішкі энергиясын өзгертуге кетеді: dQ =dU (8.19)

(8.13) формулаға сәйкес, dU_m=С_VdT, сонда газдың кез келген массасы үшін

dQ =dU=(m/m)С_VdT (8.20)

болады, яғни идеал газдың ішкі энергиясының өзгерісі оның абсолют температурасының өзгерісіне тура пропорционал.

2. Изобаралық процесс.Газдың қысымы тұрақты, яғни Р=Const болады, диаграммасы (16-сурет). Сонда 1-2 кесіндісі газдың изобаралық ұлғаюын

көрсетеді де, штрихталған аудан изобаралық жұмыстың шамасын анық-тайды: A=₁ò ² pdV=p (V₂–V₁) (8.21)

Егер газдың осы таңдап алынған екі күйі үшін Менделеев–Клапейрон тең-деуін (pV=(m/m)RT) қолданатын болсақ, онда pV₁=(m/m)RT₁ , pV₂=(m/m)RT_{2 ,} осыдан V₂ –V₁ =(m/m)(R/p)(T₂ – T₁) (8.22)

Онда изобаралық ұлғаю кезіндегі жұмыс үшін жазылған (8.21) өрнек келесі түрде жазылады: A=(m/m)R (T₂ – T₁) (8.23)

Осыдан молярлық газ тұрақтысының R физикалық мағынасы шығады: егер

T₂–T₁=1К болса, онда газдың 1 молі үшін R=A, яғни шамасы жағынан газдың 1 молін 1 К-ге қыздыру үшін қажетті жұмысқа тең.

Изобаралық процесс кезінде массасы m газға берілген жылу мөлшері

dQ=dU=(m/m)С_p dT (8.24)

болса, онда газдың ішкі энергиясы dU= (m/m) С_V dT шамаға артады. Cонда газ (8.24) формуламен есептеуге болатын жұмыс жасайды.

3. Изотермиялық процесс.Газдың температурасы тұрақты, яғни Т=Const болады, диаграммасы гипербола болады (17-сурет). Изотермиялық процесс Бойль–Мариотт заңымен өрнектелетінін білеміз PV=Const, изотермиялық процесс кезіндегі жұмысты анықтаймыз, оның шамасы суреттегі штрихталған ауданға тең. Менделеев–Клапейрон теңдеуінен (pV=(m/m)RT) және (8.21) өрнектен изотермиялық ұлғаю процесінің жұмы-сын анықтауға болады

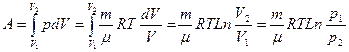(8.25)

Т=Const болғанда идеал газдың ішкі энергиясы өзгермейді: dU=(m/m)С_VdT=0, олай болса, термодинамиканың бірінші заңынан (dQ=dU+dA) изотермиялық процесс үшін dQ=dA (8.26) болады, яғни газға берілген жылудың барлық мөлшері оның сыртқы күштерге қарсы жа-саған жұмысына жұмсалады:

Q=A=(m/m)RTLn(р₁/р₂)=(m/m)RTLn(V₂/V₁) (8.27)

P P

Р₂

А

Р₁

V₁ V₂ V 0 V₁ V₂ V

17- сурет 18- сурет

5. Адиабаталық процесс.Жүйе мен сыртқы қоршаған орта арасында жылу алмаспай өтетін процесс адиабаталық процесс деп аталады (dQ=0). Барлық тез өтетін про-цестерді адиабаталық процестерге жатқызуға болады. Мысалы дыбыстың ортада таралуын адиабаталық процеске жатқызуға болады, себебі дыбыс толқындарының таралу жылдамдығы өте жоғары болғандықтан, толқын мен орта энергиясы арасында жылу алмасу болып үлгермейді. Адибаталық процестер іштен жану двигательдерінде (цилиндрлердегі жанғыш қоспалардың ұлғаюы мен сығылуы), тоңазытқыш қондырғыларында және т.б. қолданылады. Термодинамиканың бірінші бастамасын адиабаталық процесс үшін жазатын болсақ: dA=-dU (8.28), яғни сыртқы күштердің жұмысы жүйенің ішкі энергиясының өзгерісі есебінен жасалады. (8.13) және (8.1) өрнектерді қолданып, газдың кез келген массасы үшін (8.28) теңдікті жазамыз: pdV=(m/m)C_VdT (8.29)

Идеал газ күйінің теңдеуін pV=(m/m)RT дифференциалдап, келесі теңдікті аламыз: pdV+Vdp=(m/m)RdT (8.30)

Осы соңғы екі теңдіктердегі Т-ны алып тастасақ, келесі өрнек шығады:

pdV+Vdp/ pdV=R/C_V = – (C_p –C_V)/ C_V (8.31)

Айнымалыларды бөліп және C_p/C_V=g екенін ескеріп, келесі өрнекті алуға болады: dp/p=-gdV/V, Осы теңдікті p₁-ден p₂-ге және осыған сәйкес V₁-ден V₂ -ге дейінгі шектерінде интегралдап, одан кейін потенциалдасақ мынадай өрнекті аламыз: p₂/p₁=(V₁/V₂)^g немесе p₁V₁^g=p₂V₂^g

Газдың 1 және 2 күйлері еркін таңдап алынғандықтан, pV^g=Const жазуға болады. Осы алынған теңдеу адиабаталық процесс теңдеуі немесе Пуассон теңдеуі деп аталады. Мұндағы g-өлшемсіз шама, Пуассон коэффициенті деп аталады. Адиабаталық процестің диаграммасы р,V координатасында гипербола түрінде салынады (18-сурет). Суреттен байқайтынымыздай, адибата изотермаға қарағанда тіктеу келеді, себебі адиабаталық сығылу кезінде 1-3 газ қысымының ұлғаюы оның көлемінің кішіреюімен ғана емес, изотермиялық сығылудағы сияқты, температураның артуымен де байланысты.

Адиабаталық процесс кезіндегі жасалатын жұмысты есептеу үшін (8.29) теңдікті келесі түрде жазамыз dA=–(m/m)C_V dT (8.32)

Егер газ көлемі V₁-ден V₂-ге дейін адиабаталық ұлғаятын болса, онда оның температурасы Т₁-ден Т₂-ге дейін кемиді және идеал газдың ұлғаю кезіндегі жұмысы A=–(m/m)C_V ^Т2ò _Т1 dT= (m/m)C_V (Т₁–Т₂ ) (8.33)

Алдыңғы әдістерді қолдана отырып, адиабаталық ұлғаю үшін де жұмыстың формуласын келесі түрде түрлендіріп жазамыз.

A=(p₁V₁/g-1 )[1-(V₁ / V₂)^g-1]=(RT₁m/(g-1)m[1-(V₁ /V₂)^g-1] (8.34)

мұндағы p₁V₁=(m/m)RT₁ қарастырып отырған изохоралық, изобаралық, изотермиялық және адиабаталық процестердің ортақ қасиеті–олар тұрақты жылу сыйымдылықта өтеді. Алғашқы екі процесте жылу сыйымдылықтар С_V және C_P, изотермиялық процесте (dТ=0) жылу сыйымдылық ±¥, адиабаталық процесте (dQ=0), жылу сыйымдылық нольге тең. Жылу сыйымдылық тұрақты болып қалатын процесс политропты процесс деп аталады.

Термодинамиканың бірінші бастамасынан жылу сыйымдылық тұрақты болған жағдайда (С=const) политропты процесс теңдеуін қорытып шығарып алуға болады PVⁿ=const (8.35). n–политроп дәрежесі. n=(С–С_р)/(С-С_V)

6. Дөңгелек процестер (цикл).Жүйе бірнеше күйден өтіп, бастапқы күйіне қайтып келетін болса, онда процесс дөңгелек процесс (немесе цикл) деп аталады. Диаграммада дөңгелек процесс тұйық сызық түрінде көрсетіледі (19-сурет). Идеал газдың циклін газдың ұлғаюы (1-2) және сығылуы (2-1) деп екіге бөлуге болады. Ұлғаю жұмысы (1а2V₁V₂1) фигурасының ауданымен анықталады, және оң болады (dV>0). Cығылу жұмысы (2b1V₁V₂2 фигурасының ауданымен анықталады) және теріс болады (dV<0). Газдың цикл кезінде жасайтын жұмысы тұйықталған қисықпен шектелген ауданға тең, егер осы жасалған жұмыстың мәні оң болса, онда цикл тура деп аталады (цикл сағат тілінің қозғалысымен бағыттас болады, 19-сурет), ал егер жасалған жұмыстың мәні теріс болса, онда цикл кері деп аталады (цикл сағат тіліне қарсы бағытта өтеді 20-сурет),

Р Р

1 1

b

a

b a 2

V₁ V₂ V V₁ V₂ V

19- сурет 20- сурет

Тура цикл периодты түрде жұмыс істейтін және ол жұмысты сырттан алатын жылу есебінен жасайтын жылу двигательдерінде қолданады.

Кері цикл периодты түрде жұмыс істейтін және сыртқы күштердің әсерінен жасалатын жұмыс есебінен жүйе жылуы температурасы жоғары денеге тасымалданатын тоңазытқыш машиналарда қолданады.

Дөңгелек процесс нәтижесінде жүйе бастапқы күйіне қайтып келетіндіктен, ішкі энергиясының толық өзгерісі нольге тең. Сондықтан да дөңгелек процесс үшін термодинамиканың бірінші бастамасы Q=DU+A (8.36) болып жазылады, яғни цикл кезінде жасалған жұмыс сыртан алған жылуға тең болады. Дегенменен, дөңгелек процесс нәтижесінде жүйе жылуды алуы да мүмкін және сыртқа беруі де мүмкін, сондықтан Q=Q₁–Q₂ болады. Мұндағы Q₁-жүйенің алған жылуы, Q₂-жүйенің берген жылуы. Сондықтан да дөңгелек процестер үшін термиялық пайдалы әсер коэффициенті келесі формуламен есептеледі:

h=А/Q₁=(Q₁ -Q₂)/ Q₁=1–( Q₂/Q₁) (8.37)

Кері бағытта өткізуге болатын процесті тура бағытта өткізгенде жүйе қандай күйлерден өтсе, кері бағытта сондай күйлер тізбегінен өтетін процесті қайтымды процесс деп атайды. Қайтымды процестерге тепе-тең процестер жатады. Осы шартты қанағаттандырмайтын, тепе-тең емес барлық нақты процестер қайтымсыз процестер болады. Кез келген тепе-тең процестер қайтымды болады.

7. Термодинамиканың екінші бастамасы.Термодинамиканың екінші бастамасы жылу машиналарының жұмыс істеу принциптерін байқаудан қалыптасты. Сондықтан осы жылу машинасының схемасын (21-сурет ) қарастырайық. Сонда температурасы жоғары жылу көзінен бір циклде алынатын жылу мөлшері Q₁ жұмыстық денеге беріліп жұмыс өндіреді. Ал, жылу мөлшерінің бір бөлігі Q₂ суытқышқа беріліп отырады: Q₂=Q₁–А. Сөйтіп жылу двигателінде (қозғалтқыш) өндірілген жұмыс А=Q₁–Q₂. Практикалық тұрғыдан қарағанда өндірілген жұмыс қыздырғаштан алынған жылу мөлшерінің қандай бөлігі екенінің үлкен маңызы бар.

Т₁ Т₁

Q₁ Q₁

А А

Q₂ Q₂

Т₂ Т₂

21- сурет 22- сурет

Жылу машинасының термиялық пайдалы әсер коэффициенті h=1 болуы үшін Q₂=0 шарты орындалуы керек, яғни берілген жылу мөлшерінің көп бөлігі жұмысқа айналса, машинаның соғұрлым тиімді болатыны анық. Сөйтіп, жылу машинасы тек қыздырғыштан алған жылу мөлшері Q₁ арқылы жұмыс өндірер еді, ал бұл мүмкін емес. Француз инженері С.Карно 1824 жылы жылу машинасының жұмыс істеуі үшін міндетті түрде температурасы әртүрлі екі жылу көзі болуы керектігі дәлелденді.

Осы пікірді кейінірек 1851ж. Клаузиус пен Томсон дамытып, мынандай принцип түрінде тұжырымдады: нәтижесі бір жылу көзінен алынған жылу мөлшері есебінен тек жұмыс өндіру ғана болып табылатын периодты процесті жүзеге асыруға болмайды, яғни жылу көзінен жұмыстың денеге берілген жылу мөлшері толық жұмысқа айналатын машина жасау мүмкін емес. Бұл принцип термодинамиканың екінші бастамасы деп аталады. Осыдан туындайтын екінші түрдегі перпетуум мобиле жасау мүмкін емес.

Термодинамиканың екінші бастамасы өтіп жатқан процестің бағытын анықтайтындықтан, энергияның бір түрден екінші түрге ауыспайтынын көрсетеді.

8. Карно циклі.Термодинамиканың екінші бастамасына сүйене отырып, Карно мынандай теорема қорытып шығарды: барлық периодты түрде жұмыс істейтін жылу машиналарының ішіндегі ең тиімдісі–қыздырғыш пен суытқыштың температуралары бірдей және пайдалы әсер әсер коэффи-циенттері жоғары қайтымды машиналар. Олардың п.ә.к.-і машинаның конс-трукциясына тәуелді емес. Карно зерттеген циклдер өте тиімді, әрі үнемді тұйық процесс болып есептеледі. Бұл цикл екі изотерма және екі адиабата-дан құралатын қайтымды тұйық процесс. Циклді жүзеге асыру үшін, жұмыстық дене термиялық түрде ұлғайғанда оған тиісті мөлшерде жылу беріп тұратын қыздырғыш және жұмыстық дене изотермиялық түрде сығылғанда онан тиісті мөлшерде жылу алатын суытқыш болу қажет. Жұмыстық заттың ұлғайғанда өндіретін жұмысы оң, ал сығылғанда өндіретін жұмысы теріс болады. Жұмыстық зат ретінде идеал газдың 1 молін алып, идеал газға қатысты Карно циклін қарастырайық (22-сурет). Анықтама бойынша жылу машинасының п.ә.к.-і h=(Q₁–Q₂)/Q₁ (8.38)

мұндағы Q₁–циклдің ішінде қыздырғыштан алынатын жылу мөлшері де, Q₂–суытқышқа берілетін жылу мөлшері.

Изотермиялық процесте идеал газдың ішкі энергиясы тұрақты болады, сондықтан жұмыстық дене (газ) 1-күйден 2-күйге көшкенде, яғни изотермиялық ұлғайғанда (1-2) орындайтын А_1,2 жұмысына тең болады:

Q₁=A_1.2=(m/m )RT₁ Ln(V₂/V₁) (8.39)

мұндағы m-машинадағы идеал газдың массасы. Ал адиабаталық ұлғаюда (8.23), сыртқы ортамен жылу алмасу болмай, істелген жұмыс А_2,3 ішкі энергияның өзгеру есебінен пайда болады: А₂₃=-(m/m)C_V(T₂–T₁) (8.40)

Енді суытқышқа берілетін жылу мөлшері Q₂ жұмыстық затты 3-күйден 4-күйге көшіргендегі, яғни изотермиялық сығылуға жұмсалатын А₃₄ жұмысқа тең: - Q₂=А₃₄ =(m/m ) RT₁Ln(V₃/V₄) (8.41)

Ең соңында адиабаталық сығылу процесі (41) кезіндегі жұмыстың шамасы:

А_4.1 = -(m/m )C_V (T₁ – T₂) = - А₂₃ (8.42)

Тұйық процесс кезінде орындалған толық жұмыс:

А_тол = A₁₂ + А₂₃ + А_3,4 + А_4.1 = Q₁ +А_2,і - Q₂ - А_2,3 = Q₁ - Q₂

Осы А_тол. 23-суреттегі штрихталған

ауданға сәйкес келеді. Сөйтіп, Карно Р

циклінің термиялық п.ә.к. – і (8.37) 1

өрнекке сәйкес h = A / Q₁ =(Q₁ - Q₂)/ Q₁ Q⁺₁

шамасына тең болады. Енді адиабата- dQ=0 2

лық ұлғаю үшін (V₂ /V₃)^g-1= T₂ /T₁ T₁

қатынасын пайдаланып адиабаталық dQ=0

сығылу үшін (V₁ /V₄)^g-1 = T₂ /T₁ деп 4 T₂

жазайық. Осы екі қатынастың оң 3

жақтағы мүшелері тең болғандықтан, Q ₂^(-)

сол жақтары өзара тең, сондықтан:

(V₂ /V₃)^g-1=(V₁ /V₄)^g-1 , V₂/V₁ =V₃/V₄ (43). 23- сурет

(8.43) қатынасты (8.42)-ге және (8.40) пен (8.41) өрнектерді (8.37) теңдеуге қойсақ, п.ә.к.-і:

h=(Q₁-Q₂)/Q₁=((m/m)RT₁Ln(V₂/V₁)-(m/m)RT₂Ln(V₃/V₄))/((m/m)RT₂Ln(V₂/V₁))(44)

Сонымен, идеал газға арналған Карно циклінің п.ә.к.-і тек қыздырғыш пен суытқыш температурасына байланысты. Карноның бұл қарастырған тура циклі идеал түрдегі жылу машинасы болып табылады. Толық бір цикл өткенде газдың өндіретін жұмысы: А=Q₁ –Q₂=hQ₁ (8.45)

Әдетте қыздырғыштың температурасы суытқыштың температурасынан әлдеқайда көбірек болса ғана п.ә.к.-нің мәні көп болады. Егер Т₂=0 болса, онда h=1 болады.

Карно циклі қайтымды болғандықтан, оны керісінше жүргізуге де болады

(23-сурет). Карноның мұндай кері циклі идеал түрдегі суытқыш машина болып табылады. Оның беретін жылу мөлшерін мына формула арқылы есептеп табуға болады: Q₂ = (1-h)А/h (8.46)

Сөйтіп, Карноның тұжырымдауынша термодинамиканың екінші бастамасы-на былайша анықтама беруге болады: ешуақытта суығырақ денеден ысты-ғырақ денеге жұмыс өндірілмей жылу мөлшерінің берілуі мүмкін емес.

9. Энтропия.Молекулалардың қозғалысы кезінде, олардың ретсіздікте-рін ықтималдылық теориясымен сипаттау өте тиімсіз. Сондықтан біз n бөліктен құралған жүйені қарастырайық, олардың ықтималдылық саны N₁, N₂, N₃, ..., N_n болсын. Толық жүйе үшін оның ықтималдылығы

N = N₁ · N₂ · N₃ ·, ..., · N_n

Жүйені толық сипаттау үшін оны түзетін бөліктерінің ықтималдылығының көбейтінділерін емес, олардың қосындысын аламыз. Ол үшін Больцман тағайындаған заң бойынша молекулалардың жылулық қозғалысының ретсіздік мөлшерін белгілі бір функция арқылы сипаттауға болады: S=kLnN, мұндағы: N-берілген күйдің ықтималдылығы, k-Больцман тұрақтысы, S-берілген жүйе өзгерісін сипаттайтын функция-энтропия деп аталады. Толық жүйе үшін, оның күйінің ықтималдылығы LnN=LnN₁+LnN₂+LnN₃+…LnN_n. Жүйенің энтропиясын былайша анықтаймыз: S=kLnN=kLnN₁+kLnN₂+kLnN₃+…+kLnN_n, S=S₁+S₂+S₃+…+S_n

Егер жүйе күйінің өзгерісі тек қана бір әдіспен жүзеге асатын болса, онда оның ықтималдылығы N=1, энтропиясы S=kLnN=0 болады. Мысалға кез келген реттелген механикалық қозғалысты алуға болады. Шынында қатты дененің айналысы кезінде оның барлық молекулалары бірдей бұрыштық жылдамдықпен қозғалады.

Оқшауланған жүйеде қайтымсыз процесс кезінде жүйенің энтропиясы артады. Сонымен қатар оқшауланған жүйеде процестер энтропия артатын жаққа қарай бағытталады: DS>0 (8.38)

дербес жағдайда жүйеде өтетін процестердің барлығы да қайтымды болғанда энтропия өзгермейді DS=0 (8.39)

қарастырылып отырған процестер қайтымды болса, онда энтропия өзгермей тұрақты болады, ал қайтымсыз процестер үшін ылғи артып отырады

DS ³ 0 (8.40)

Бұл Клаузиус теңдеуі деп аталады. Енді энтропияның математикалық өрнегін жазу үшін (8.37) теңдеуді түрлендіріп жазайық:

(Q₁ -Q₂)/Q₁=(T₁-T₂)/T₁, 1–(Q₂/Q₁) =1-T₂/T₁ немесе Q₂/Q₁=T₂/T₁,

Q₁/T₁= Q₂/ T₂=0, мұндағы Q₂ жұмыстық дененің суытқышқа беретін жылу мөлшері болғандықтан, теріс шама болып есептеледі, сондықтан:

Q₁/T₁+Q₂/T₂=0 (8.41)

Q/Т-келтірілген жылу мөлшері деп аталады. Осы келтірілген жылу мөлшері, процестегі денеге өте аз мөлшерде берілетін болса, онда оның мәні dQ/T болады.

Кез келген қайтымды тұйық процестер үшін келтірілген жылу мөлшері-нің жалпы қосындысы нольге тең болады, яғни интеграл процестің жүріп өтетін процестің жолына тәуелді болмайтындығын көреміз. сонымен энтро-пияның өзгерісін мына формула арқылы анықтаймыз Q/T=dS (8.42)

Энтропия да жүйе күйін сипаттайтын шама. Өлшем бірлігі- Дж/(моль·К)

Егер тепе-тең жағдайдағы жүйе 1-күйден 2-күйге өтетін болса, онда энтропия өзгерісі (18-сурет):

D S_1®2 = S₂ – S₁ =₁ò ² dQ /T=₁ò ²(dU+dA) /T (8.43)

яғни, бұл айырма 1-және 2-күйлердің арасында өтетін кез келген қайтымды процесте жылудың келтірілген мөлшерінің қосындысына тең болады. Жоға-рыда айтылғандай энтропияның абсолют мәнін анықтауға мүмкіндік жоқ, тек 1-және 2-күй энтропияларының (S₂–S₁) айырымын ғана тағайындауға болады. Жоғарыда айтылған идеал газ үшін ішкі энергияның, жұмыстың формулаларын және (8.43) формуланы қолдана отырып энтропия өзгерісі-нің формуласын жазуға болады:

DS_1®2 =S₂–S₁=(m/m )(C_VLn(T₂/T₁)+RLn(V₂/V₁) (8.44)

Сөйтіп, идеал газ энтропиясының өзгерісі DS_1®2 жүйе 1–күйден 2-күйге ауысқанда, процестің өту тәртібіне тәуелді болмайды.

Оқшауланған жүйе жағдайында ол тұтас алғанда, яғни адиабаталық процесс үшін жылу алмайды да бермейді де: dQ=0, DS=0, S=Const

Сонда адиабаталық қайтымды процестер энтропия тұрақты болғанда ғана өте алады. Ал изотермиялық процестер кезінде T₁=T₀ болғандықтан, энтропия өзгерісі: DS=(m/m)RLn(V₂/V₁), ал изохоралық (V₁=V₂) процесс үшін энтропия өзгерісі DS=(m/m)C_VLn(T₂/T₁)

10. Термодинамиканың үшінші бастамасы.Барлық оқшауланған жүйеде қайтымсыз процестер өткенде жүйе энтропиясы артады. Энтропия реттелмеген, ретсіз жүйе мөлшерін көрсетеді. Энтропияның абсолют мәндерін анықтау үшін оның ең болмағанда қандай да бір белгілі температура кезіндегі абсолют мәнін білуіміз керек. Энтропияның мұндай мәнін Нернст ұсынған термодинамиканың үшінші бастамасы деп аталатын теорема анықтап береді. Нернст теоремасы бойынша температура абсолют ноль болғанда қандай дененің болмасын энтропиясы нольге тең. Бұл қағи-даны былайша түсіндіруге болады. Клаузиустың ұйғаруынша, егер бүкіл әлем кеңістігін оқшауланған жүйе деп қарастырып, оған термодинамиканың екінші бастамасын қолдансақ, онда оның энтропиясы бара-бар өзінің ең жоғарғы максимум мәніне жетуі керек, сөйтіп барлық қозғалыс түрі келешекте жылуға ауысып, барлық ыстығырақ денелердің температуралары суығырақ денелерге өтіп, әлемде тепе-теңдік күй қалыптасады. Оның салда-рынан әлем кеңістігіндегі барлық процестер тоқталып, жылулық апат қаупі туады деді. XIX ғасырда айтылған осы пікірдің бір кемшілігі термодинамиканың екінші бастамасын сол кездегі кейбір оқымыстылар (идеалистер) шегі жоқ және үздіксіз қозғалыста, дамуда болатын әлем кеңістігіне қодануға болмайтынын түсінбеді. Кейінірек көптеген ғалымдар (материалистер) XIX ғасырдың аяғы мен XX ғасырдың басында бұл пікірді жоққа шығарды.