Средства обеспечения дисциплины 10 страница

Лекция №8. Механика деформируемых тел

1. Упругие силы

Упругие силы действуют со стороны деформированного тела на тело, непосредственно соприкасающееся с этим деформированным телом. Данные силы действуют также со стороны деформированной части тела на другие смежные части этого же тела.

Под деформацией подразумевается изменение взаимного расположения точек тела.

Деформации сопровождаются изменением геометрической формы тела и его размеров.

На данное тело упругими силами могут действовать твердые, жидкие и газообразные тела. Упругие силы в твердых телах возникают как при изменении их формы, так и при изменении объема. В жидкостях упругие силы возникают лишь при изменении объема жидкости. Газ всегда действует упругими силами на стенки сосуда, в котором он находится, величина этих сил зависит от объема сосуда.

Упругие силы представляют собой проявление сил взаимодействия молекул, составляющих твердые, жидкие и газообразные тела. В конечном счете, происхождением они обязаны электрическому взаимодействию между частицами, входящими в состав молекул. Силы молекулярного взаимодействия очень быстро убывают с увеличением расстояния между молекулами и радиус действия их не более 10^-7 – 10^-8 см. Поэтому упругими силами взаимодействуют между собой только тела, находящиеся в непосредственном контакте.

Упругая сила действует только со стороны деформированного тела. Действительно, если тело не подвергается действию внешних сил, то каждая молекула тела находится в равновесном положении. При деформации тела изменяется положение каждой молекулы относительно соседних. Молекулы, находящиеся от данной молекулы на расстояниях, меньших равновесного, действуют на неё силами отталкивания, а молекулы, находящиеся на расстояниях, больших равновесного, – силами притяжения. В результате действия совокупности молекул, сдвинутых со своих равновесных положений, возникает сила, действующая на тело, непосредственно соприкасающееся с данным. Это и есть упругая сила.

Упругие силы возникают лишь при таких деформациях, когда при прекращении действия на тело внешних сил деформация исчезает, т.е. тело восстанавливает свою первоначальную форму и размеры. Такие деформации называются упругими.

Опыт показывает, что сила упругости 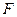, возникающая при малых деформациях любого вида, пропорциональна величине деформации :

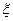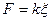(8.1)

Это положение называется законом Гука.

Коэффициент пропорциональности k зависит от свойств тела, подвергающегося деформации (его размеров, формы, вещества, из которого оно изготовлено), от вида деформации, от выбора величины, характеризующего деформацию, а также от температуры.

В качестве примера тела, действующего на другие тела упругой силой, рассмотрим пружину. Закон Гука для пружины имеет вид: 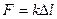, где 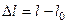– деформация пружины, равная изменению её длины, причем 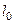– длина недеформированной пружины, – длина деформированной (растянутой или сжатой). Коэффициент называется коэффициентом жесткости пружины. Он показывает, какую силу нужно приложить к данной пружине для её растяжения на единицу. Величина этого коэффициента зависит от числа витков, их диаметра, материала проволоки, из которой изготовлена пружина, и диаметра этой проволоки.

Направления сил упругости и деформаций противоположны. Рассмотрим пружину, один конец которой закреплен, а на другой конец прикреплено тело. Выберем систему координат, одна из осей которой (например, ось Х) направлена вдоль пружины, а начало её связано с концом недеформированной пружины. Тогда при смещении тела вдоль оси Х на некоторое расстояние деформация пружины, прикрепленной к этому телу, будет равна координате 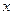этого тела. В этом случае упругая сила, действующая на тело со стороны пружины, будет иметь проекцию 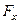, которая согласно закону Гука равна

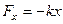(8.2)

Знак минус показывает, что при смещении тела в положительном направлении оси Х проекция силы на эту же ось имеет отрицательное направление.

Упругие силы относятся к центральным силам, так как при любом положении тела деформация тела определяется координатой х.

Действие на твердое тело упругих сил со стороны других твердых тел проявляется в виде силы нормального давления. Например, на тело, лежащее на столе, действует упругая сила со стороны стола.

Твердые тела, действующие на некоторое тело упругими силами, могут ограничивать его движение. Например, такими ограничивающими движение телами являются рельсы, плоскости, по которым скользит тело, нити, связывающие тело с другими телами, оси, закрепленные в подшипниках и т.д. Тела, ограничивающие движение данного тела, называют связями, а упругие силы, которыми они действуют на это тело – силами связей или силами реакций. Измерить их практически невозможно, однако можно найти при помощи законов Ньютона, учитывая ограничения, накладываемые этими связями на движение тел. Например, тело соскальзывает с наклонной плоскости без трения. На тело действует сила тяжести, направленная вниз, и упругая сила связи (реакции) со стороны наклонной плоскости, направленная перпендикулярно поверхности соприкосновения тела и плоскости в сторону тела. Сила связи в уравнениях Ньютона фигурирует в качестве неизвестных.

2. Виды упругих деформаций

Деформации зависят от многих причин:

- от формы и размеров деформируемого тела;

- от величины, направления и точек приложения внешних сил;

- от свойств вещества, из которого изготовлено тело;

- от того, движется ли тело или оно неподвижно;

- от температуры.

Все эти причины могут комбинироваться самым различным образом. Поэтому виды деформаций весьма разнообразны.

Мы будем считать, что:

- деформированное тело неподвижно;

- деформируемое тело однородное, т.е. свойства вещества во всех точках тела одинаковы;

- температура деформируемого тела во всех его точках одинакова и постоянна;

- деформации малы, т.е. смещения точек тела относительно друг друга малы по сравнению с расстоянием между этими точками.

Существует несколько видов деформаций тел: одностороннее сжатие или растяжение, всестороннее растяжение или сжатие, кручение, сдвиг, изгиб. Каждый вид деформации вызывает появление соответствующей силы упругости. Однако все виды деформаций можно свести к двум видам: растяжению (или сжатию) и сдвигу.

Рассмотрим эти основные деформации несколько подробнее.

Пусть стержень длины 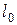и поперечного сечения 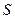подвешен (рис. 8.1). Под влиянием деформирующей силы 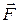он растягивается, приобретает новую длину и в нем возникает сила упругости .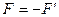

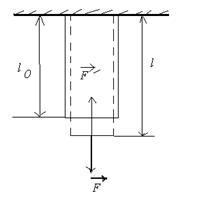
Рис.8.1.

Мерой деформации растяжения может служить величина 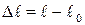– изменение длины стержня, которую называют абсолютным удлинением. Другой величиной, характеризующей деформацию стержня, является относительное удлинение (удлинение каждой единицы длины стержня): .

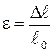Опыт показывает, что относительное удлинение стержня пропорционально деформирующей силе и обратно пропорционально площади поперечного сечения

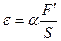, (8.3)

где a – коэффициент упругости при растяжении (сжатии) или коэффициент продольного удлинения (сжатия), зависящий только от материала стержня.

Отношение силы к сечению, на котором она действует, называется напряжением в данном сечении. Деформацию растяжения вызывает сила, нормальная к площади сечения, а возникающее напряжение называется нормальным напряжением р_n:

р_n = 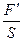(8.4)

В физической литературе напряжение, определяемое по формуле (8.4), называют также натяжением, если тело растягивают. Его обозначают буквой Т.

Тогда закон Гука для деформации растяжения (сжатия) примет вид:

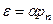(8.5)

При р_n=1 a =e, т.е. коэффициент упругости численно равен относительному удлинению стержня, происходящему под действием единичного напряжения.

Для характеристики упругих свойств материала пользуются величиной 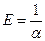, которая называется модулем упругости или модулем Юнга. Эта величина измеряется в Паскалях. Согласно формулам (8.4) и (8.5),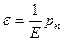

В качестве характеристики деформации сдвига берется величина

Е = р_nпри e=1, т.е. модуль Юнга численно равен тому напряжению, которое вызывает единичное относительное удлинение, или абсолютное удлинение, равное длине стержня. Решив уравнение (8.3) относительно деформирующей силе и учитывая формулы (8.4) и (8.5), получим выражение

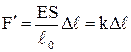(8.6)

где k– постоянный для данного стержня коэффициент. Соотношение (8.6) выражает закон Гука для стержня.

Опыт показывает, что под действием растягивающей силы изменяются не только продольные, но и поперечные размеры стержня. Если сила растягивающая, то поперечные размеры стержня уменьшаются. Пусть до деформации толщина стержня равна а₀, а после деформации – а. Если сила растягивающая, то величина 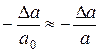называется относительным поперечным сжатием стержня. Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона: .

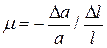Рассмотрим деформацию сдвига. Возьмем однородное тело, имеющее форму прямоугольного параллелепипеда, нижнюю грань закрепим, а к его верхней грани приложим силу F,параллельную нижней грани.

Рис.8.2

Если действие силыFбудет равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникнет тангенциальное напряжение, т.е. напряжение, при котором сила направлена по касательной к поверхности, на которую она действует: 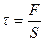, где S– площадь грани. Под действием напряжений тело деформируется так, что одна грань сместится относительно другой на некоторое расстояние а. Если тело мысленно разбить на элементарные, параллельные рассматриваемым граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев. Поэтому деформация такого типа называется сдвигом.

При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, повернется на некоторый угол j. В качестве характеристики деформации сдвига берется величина

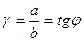, (8.7)

называемая относительным сдвигом. При упругих деформациях угол jбывает очень мал. Поэтому можно положить tgj»j. Следовательно, относительный сдвиг gоказываетсяравным углу сдвига j.

Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению: .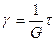

Коэффициент Gзависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45⁰ (tgj=1), если бы при сколь угодно больших деформациях не был превзойден предел упругости. Измеряется Gкак и Е в Паскалях. Для большинства упругих тел G@0,4E.

3. Упругие и пластические деформации.
Предел упругости и предел прочности

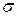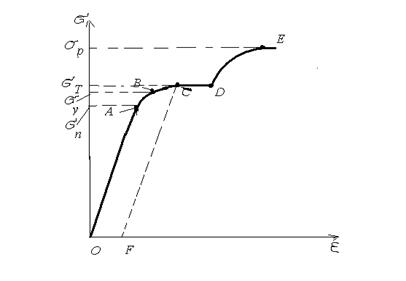
Деформации твердых тел подчиняются закону Гука до известного предела. Обозначим в общем случае напряжение через . Связь между относительной деформацией и напряжением 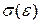представляется в виде диаграммы напряжений, которую мы качественно рассмотрим для твердого тела (рис.8.3).

Из рисунка видно, что линейная зависимость, установленная Гуком, выполняется лишь для упругих тел при малых относительных деформациях, а именно до так называемого предела пропорциональности 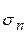, соответствующая области ОА. При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость 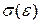уже не линейна) и до предела упругости 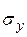остаточные деформации не возникают.

Рис.8.3

Предел упругости практически совпадает с точкой В. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ОВ, а параллельной ей – СF. Фигура OABCFO называется областью упругого гистерезиса. Напряжение, при котором появляется заметная остаточная деформация ( 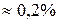), называется пределом текучести . Ему соответствует точка С на кривой. В области СD деформация возрастает без увеличения напряжения, т.е. тело как бы “течет”. Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, если же она практически отсутствует – хрупкими. Деформация не исчезает и после прекращения воздействия на тело, когда она достаточно велика. Тогда деформацию называют пластической (текущей), в области которой лежит точка С.

При дальнейшем растяжении происходит разрушение тела. На рисунке в точке Е наступает разрыв. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности ( ).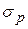

Отметим, что и в случае упругой деформации первоначальная форма тела восстанавливается не мгновенно, а через некоторое время, измеряемое иногда часами и даже днями. Это явление называется упругим последействием.

4. Всестороннее растяжение и сжатие

Допустим, что однородное изотропное твердое тело имеет форму прямоугольного параллелепипеда, к противоположным граням которого приложены силы 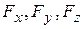, нормальные к этим граням. Соответствующие им натяжения обозначим 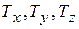(рис.8.4). Определим деформации, которые возникнут под действием этих сил. Будем предполагать деформации малыми.

Направим координатные оси параллельно ребрам параллелепипеда. Пусть 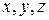– длины этих ребер. Если бы действовала только сила 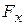, то ребро получило бы приращение 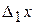. Его значение определяется из соотношения 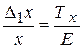. Если бы действовала только сила 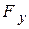, то размеры параллелепипеда, перпендикулярные оси Y, сократились бы. В частности, ребро х при этом получило бы отрицательное приращение 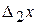, которое можно вычислить по формуле 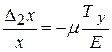. Наконец, относительное приращение ребра под действием одной только силы было равно .

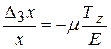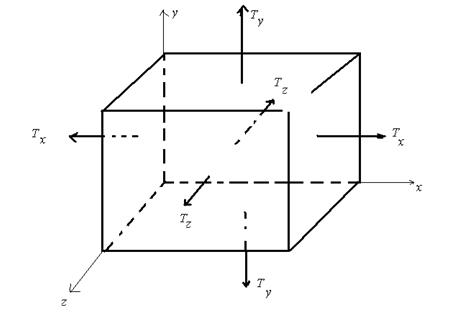
Рис. 8.4

Если бы все силы действовали одновременно, то согласно принципу суперпозиции малых деформаций результирующее удлинение ребра будет равно 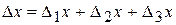. Аналогично вычисляются удлинения параллелепипеда, и вдоль остальных его ребер можно написать:

,

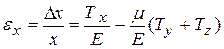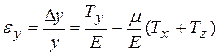, (8.8)

.

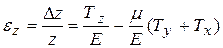Рассмотрим частный случай, когда все натяжения 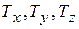равны и отрицательны. В этом случае на параллелепипед со всех сторон действует постоянное давление 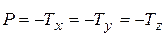. Как видно из формул (8.8), все три относительные деформации 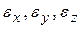равны между собой и определяются выражением

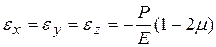(8.9)

Их можно выразить через относительные изменения объема параллелепипеда при деформации. Действительно, взяв логарифмические производные от обеих частей равенства 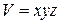, получим 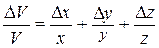или .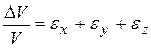

Поэтому формулу (8.9) можно представить в виде

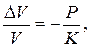(8.10)

где постоянная К определяется выражением

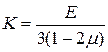(8.11)

Эта постоянная называется модулем всестороннего сжатия.

Формула (8.11) применима к телам не только прямоугольной, но и произвольной форм. Для доказательства достаточно заметить, что произвольное тело можно разделить на малые части, каждая из которых имеет форму прямоугольного параллелепипеда. Эти части находятся под постоянным внешним давлением. Относительное изменение их объемов, а следовательно, и относительное изменение объема всего тела одинаковы и определяются формулой (8.10).

5. Энергия упругой деформации

Любое упруго деформированное тело обладает потенциальной энергией,так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.

Растяжение будем производить очень медленно, чтобы силу 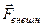, с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе 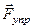. Тогда 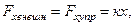где к, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна

(8.12)

Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид

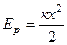, (8.13)

если считать, что потенциальная энергия недеформированной пружины равна нулю.