Средства обеспечения дисциплины 8 страница

β

Рис. 7.5. б)

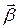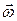Найдем связь векторов между и с величинам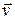и и 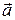. Возьмем какую-либо произвольную точку этого тела, отстоящую от оси вращения на расстоянии R. Ранее было показано, что линейная и угловая скорости точки связаны соотношением

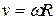(7.10)

Будем определять положение точек тела с помощью радиус-вектора 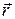, проведенного из точки, лежащей на оси вращения. На рис.7.6 видно, что 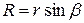. Постановка этого значения в (7.6) дает .

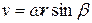Это равенство и показанные на рис. 7.6 взаимные направления векторов 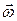, 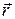и 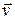дают основания представить 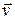в виде векторного произведения 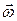на :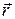

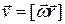(7.11)

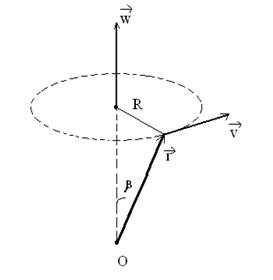
Рис.7.6

Связи модулей нормального 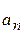и тангенциального 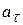ускорений с угловым ускорением 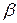и угловой скоростью 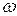имеют вид

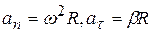(7.12)

Заметим, что последняя формула в (7.12) справедлива для случая, когда ось вращения, а, следовательно, и вектор 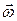, не изменяет направления в пространстве.

5. Плоское движение твердого тела

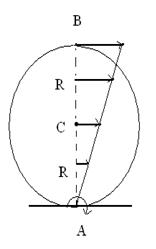
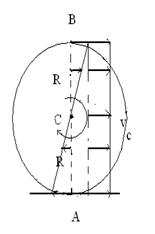
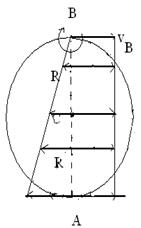
Плоским называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Произвольное плоское движение можно представить как совокупность поступательного движения и вращения. Разбиение движения на поступательное и вращательное можно осуществить множеством способов (рис. 7.7).

Рис.7.7 а	Рис.7.7 б	Рис.7.7 в

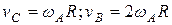
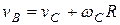
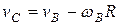
В качестве примера рассмотрим качение цилиндра радиуса 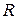без скольжения по плоскости. Скорости точек цилиндра можно представить как обусловленные: а – одним лишь вращением вокруг оси А с угловой скоростью 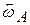(рис.7.7 а); б – поступательным движением со скоростью 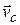и вращением вокруг оси С с угловой скоростью 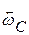(рис.7.7 б); в – поступательным движением со скоростью 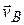и вращением вокруг оси В с угловой скоростью 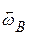(рис.7.7 в). Из приведенных на рисунке соотношений легко получить, что 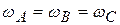. Следовательно, рассмотренные в этом примере способы отличаются значениями скорости поступательного движения, но соответствуют одной и той же угловой скорости 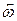. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая, через какую точку проходит ось вращения.

Возьмем скорость поступательного движения равной 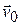. Примем одну из точек, лежащих на оси вращения, за начало координат О. Обозначим через 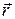– радиус-вектор, проведенный из точки О в данную точку тела. Согласно формуле (7.11), составляющую скорости точек, обусловленную вращением, можно представить в виде .

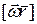Следовательно, для скорости точек тела относительно неподвижной системы отсчета получается формула

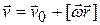(7.13)

Особенно удобным оказывается разбиение произвольного плоского движения на поступательное, происходящее со скоростью центра масс 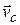, и вращение вокруг оси, проходящей через этот центр (рис. 7.7 б).

Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг так называемой мгновенной оси вращения (рис. 7.7 а). Эта ось может находиться внутри либо вне тела. Положение мгновенной оси относительно неподвижной системы отсчета и относительно тела, вообще говоря, изменяется со временем. В случае, изображенном на рис. 7.7 а-в, мгновенная ось совпадает с линией касания цилиндра с плоскостью (ось А). Эта ось перемещается как по плоскости (т.е. относительно системы отсчета), так и по поверхности цилиндра. Таким образом, плоское движение можно рассматривать как ряд последовательных элементарных вращений вокруг мгновенных осей.

6. Момент силы относительно оси

Как показывает опыт, результат действия силы при вращательном движении зависит от величины силы, от расстояния между осью (или точкой), вокруг которой вращается тело, и точкой приложения силы, а также от направления силы. Действительно, каждый по своему опыту знает, что, закрывая дверь, следует нажимать на неё подальше от оси её вращения. Кроме того, известно, что нельзя закрыть дверь, действуя на неё силой, направленной вверх вдоль оси двери, или силой, перпендикулярной оси в плоскости двери. Дверь закрывают, нажимая на неё перпендикулярно её плоскости. Когда сила приложена к одной из точек твердого тела, вектор момента силы 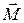характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтому момент силы называют также вращающим моментом.

Рассмотрим момент силы относительно оси. Проекция вектора 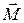на произвольную ось, проходящую через точку О, называется моментом силы относительно этой оси:

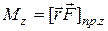(7.14)

Пусть твердое тело произвольной формы вращается под действием силы 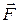вокруг некоторой неподвижной оси ОО¢ (рис. 7.8).Тогда все ее точки описывают окружности с центрами на этой оси. В качестве оси может быть взята реальная ось, вокруг которой вращается тело. Но это может быть одна из осей координат и вообще любая воображаемая прямая. Разложим действующую силу 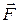на три взаимно перпендикулярные составляющие: 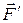(параллельную оси), 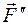(перпендикулярную оси и лежащую на линии, проходящей через ось) и 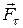(перпендикулярную 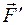и 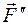). Очевидно, что вращение вызывает только составляющая 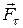, являющаяся касательной к окружности, описываемой точкой приложения силы. Эта сила называется вращающей силой. Остальные две силы вращения не вызывают. 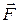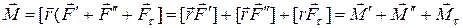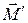Воспользовавшись определением момента силы относительно точки, представим момент силы относительно точки О в виде , где – момент силы 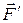и т.д.

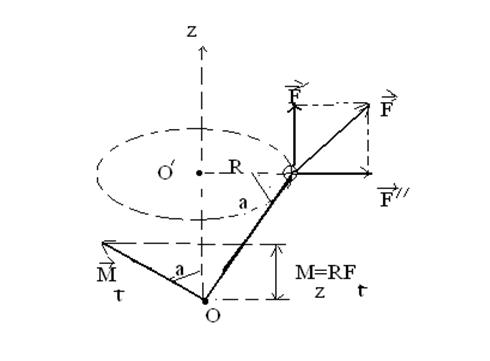
Рис. 7.8

Проекция на ось z вектора 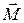равна сумме проекций моментов составляющих сил. Моменты 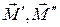перпендикулярны к оси z , поэтому их проекции равны нулю. Следовательно,

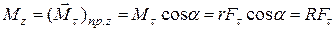(7.15)

Таким образом, моментом силы относительно оси (или моментом вращающей силы) будем называть произведение вращающей силы на радиус окружности, описываемой точкой приложения силы.

В общем случае момент силы формально определяется по той же формуле (6.29). Поэтому момент силы относительно оси представляет собой вектор, направленный перпендикулярно плоскости окружности, т.е. вдоль оси по правилу буравчика.

7. Момент пары сил

Две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой, называются парой сил (рис.7.9). Расстояние между прямыми, вдоль которых действуют силы, называется плечом пары. Суммарный момент сил относительно точки О равен

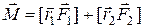(7.16)

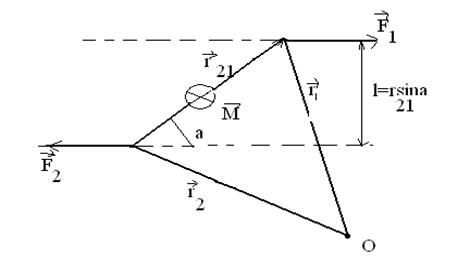
Рис. 7.9.

Учитывая, что 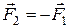, можно написать

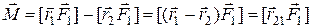, (7.17)

где 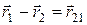(рис. 7.9).

Полученное выражение не зависит от положения точки О. Следовательно, момент пары сил относительно любой точки будет одним и тем же. Вектор перпендикулярен к плоскости, в которой лежат силы, а его модуль равен произведению модуля любой из сил на плечо. Силы гравитационного и кулоновского взаимодействия между двумя частицами образуют пару с плечом, равным нулю. Поэтому их суммарный момент относительно любой точки равен нулю. Отсюда следует, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю

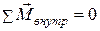(7.18)

Соответственно, равен нулю и суммарный момент относительно любой оси z:

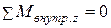(7.19)

8. Второй закон Ньютона для вращающегося твердого тела

Установим связь между угловым ускорением твердого тела и моментами сил, действующих на него, при вращении этого тела вокруг неподвижной оси. Для этого разобьем тело на элементы, каждый из которых можно принять за материальную точку. Пусть число этих элементов N. Все элементы движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на этой оси и имеют одинаковые ускорения.

Рассмотрим элемент с номером i , масса которого 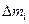, а радиус окружности, по которой он движется 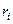. На этот элемент со стороны других элементов этого же тела действуют внутренние силы 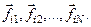Кроме того, он подвергается действию внешних сил, равнодействующая которых 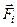. Для этого элемента справедлив второй закон Ньютона:

(7.20)

Возьмем проекцию этого уравнения на направление касательной к окружности, по которой движется элемент

(7.21)

Умножим обе части уравнения (7.21) на 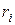и, принимая во внимание, что тангенциальное ускорение элемента представляется в виде 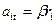, получим

(7.22)

Каждый член в правой части этого уравнения есть момент соответствующей силы относительно оси вращения z. Так, последний член 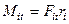– момент равнодействующей внешних сил, действующих на элемент тела, а остальные члены – – моменты внутренних сил. Величина 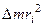, входящая в левую часть уравнения (7.22), называется моментом инерции 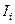этого элемента относительно оси вращения z.

С учетом введенных обозначений уравнение (7.22) можно переписать в виде: .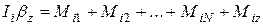

Аналогичные уравнения можно написать для каждого элемента тела, а затем их сложить. Тогда получим:

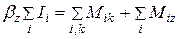, (7.23)

где в левой части имеем сумму моментов инерции всех элементов тела относительно оси вращения: .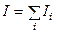

Он характеризует распределение массы тела относительно оси вращения.

В правой части первое выражение характеризует сумму моментов всех внутренних сил, действующих на все элементы тела, а последнее выражение есть сумма всех действующих на тело внешних сил .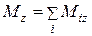

Так как при сложении моментов внутренних сил в уравнении (7.23) все они попарно уничтожаются, уравнение (7.23) принимает вид

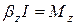(7.24)

Уравнение (7.24) есть выражение основного закона вращательного движения: Момент вращающей силы, приложенной к телу, равен произведению момента инерции тела на его угловое ускорение.

9. Момент инерции твердого тела

Из формулы (7.24) видно, что угловое ускорение, сообщаемое телу вращающим моментом, зависит от момента инерции тела; чем больше момент инерции, тем меньше угловое ускорение. Следовательно, момент инерции характеризует инерционные свойства тела при вращательном движении, как и масса при поступательном движении. В отличие от массы тела момент инерции зависит от радиуса окружности, описываемой точкой приложения силы, а, следовательно, от выбора оси вращения.

Из формулы следует, что единицей измерения момента инерции является кг.мІ.

Из определения момента инерции

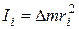(7.25)

видно, что момент инерции есть величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей:

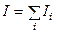(7.26)

Момент инерции существует безотносительно к вращению. Каждое тело независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Для неоднородных тел и тел неправильной формы момент инерции определяют экспериментально, а для однородных тел геометрически правильной формы – посредством интегрирования.

Как было ранее указано, в силу формулы (7.3) элементарная масса 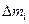равна произведению плотности тела 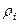в данной точке на соответствующий элементарный объем: .

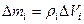Следовательно, момент инерции можно представить в виде: .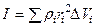

Если плотность r тела постоянна, её можно вынести за знак суммы задача нахождения моментов инерции сводится к интегрированию:

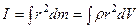(7.27)

Интегралы в (7.27) берутся по всему объему тела. Величины r и r в этих интегралах являются функциями точки.

В качестве примера вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 7.10).

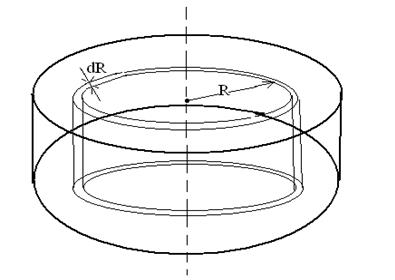
Рис. 7.10.

Разобьем диск на кольцевые слои толщиной 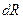. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном 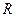. Объем такого слоя равен 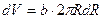, где 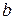– толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова, (7.27) можем вынести за знак интеграла: 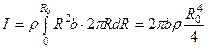, где 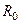– радиус диска.

Так как масса диска 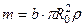, то получим

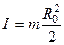(7.28)

Для однородных и симметричных тел обычно основной осью вращения является ось симметрии. В этом случае момент инерции, как мы видели, легко вычисляется.

Для некоторых тел правильной формы значение моментов инерции относительно осей, проходящих через центр их симметрии приведены в таблице 2.

Таблица 2

Форма тела	Расположение оси	Величина момента инерции
Обруч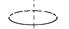
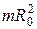
Цилиндр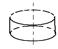
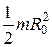
Шар
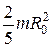
Примечание: m – масса тела, R0 – его радиус

10. Теорема Штейнера

Рассмотрим произвольное тело и две параллельные друг другу оси, одна из которых (ось С) проходит через центр масс тела, а другая (ось О) отстоит от первой на расстояние а (рис. 7.11). Выберем оси координат 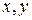и 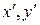так, как показано на рис. 7.11.

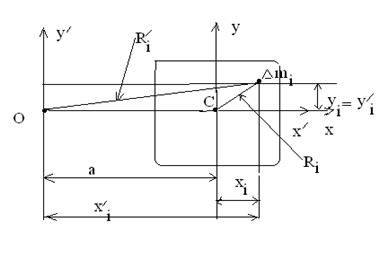
Рис. 7.11

Момент инерции относительно оси О определяется выражением

Разобьем это выражение на три суммы:

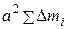
Первая сумма представляет собой момент инерции относительно оси, проходящей через центр масс. Сумма 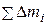дает массу тела 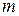. Наконец, 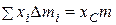, где 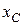– координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:

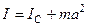(7.29)

Это соотношение выражает теорему Штейнера, которая гласит, что момент инерции 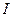относительно произвольной оси равен сумме момента инерции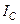относительно оси, параллельной данной и проходящей через центр масс тела, и произведением массы т тела на квадрат расстояния а между осями.

В соответствии с теоремой Штейнера момент инерции диска относительно оси ОґОґ, отстоящей на расстоянии 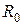от оси, проходящей через центр масс,равен найденному нами моменту инерции (7.28) относительно оси, проходящей через центр диска, плюс : .

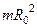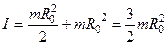11. Закон сохранения момента импульса при вращательном движении

Сравним попарно между собой законы и формулы механики поступательного движения и механики вращательного движения: второй закон Ньютона – с основным законом динамики вращения, закон изменения импульса – с законом изменения момента импульса при вращении, выражение линейной скорости – с угловой скоростью и т.д. Бросается в глаза большое сходство в формулировках сравниваемых законов и в структуре сравниваемых формул. Каждой физической величине, характеризующей поступательное движение, соответствует определенная физическая величина, характеризующая вращательное движение. Эти примеры для наглядности представлены в таблице.

Поступательное движение	Вращательное движение
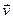Время…………………………..t Радиус-вектор………………… Линейная скорость ………….. Линейное ускорение ………… Масса…………………………. Сила…………………………... 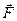Второй закон Ньютона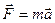	Время…………………………t Угол поворота……………… 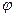Угловая скорость…………... 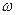Угловое ускорение………… 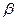Момент инерции…………… 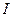Момент силы относительно оси 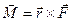Уравнение моментов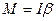

Обнаруженное сходство с законами поступательного движения характерно для всех законов вращательного движения. Пользуясь этим, напишем закон вращательного движения, аналогичный закону сохранения импульса материальной точки:

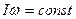, (7.30)

или для системы тел:

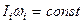(7.31)

Выражение (7.31) носит название закона сохранения момента импульса: в изолированной системе сумма моментов импульса всех тел – величина постоянная.

Из формулы (7.30) следует, что изменение момента инерции тела должно сопровождаться изменением угловой скорости вращения тела: увеличение (уменьшение) момента инерции вызывает соответствующее уменьшение (увеличение) угловой скорости. Это следствие рассматриваемого закона доказывает в частности «скамья Жуковского».

Человек с расставленными в стороны руками вращается, стоя на скамье Жуковского. Затем он быстро опускает руки. При этом его момент инерции уменьшается, а угловая скорость увеличивается. На законе сохранения импульса основаны акробатический прием «сальто-мортале», балетный прием «пируэт» и т.п. Все свободные гироскопы действуют на основе этого закона: вращающаяся с большой скоростью масса сохраняет постоянным ось своего вращения. Этим объясняется устойчивость оси Земли, вертикальная устойчивость движущегося велосипеда и т.п.

12. Кинетическая энергия вращающегося тела

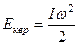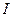По аналогии с поступательным движением запишем выражение: , где – момент инерции, 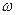– угловая скорость вращения тела.

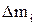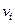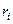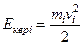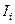Действительно, кинетическая энергия одной частицы вращающегося тела массой , движущейся со скоростью по окружности радиусом , равна , где – момент инерции частицы, 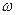– угловая скорость вращения тела. Тогда, суммируя энергии всех частиц, составляющих тело, получим выражение кинетической энергии вращающегося тела:

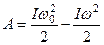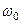За счет кинетической энергии вращения тело может совершать работу. Эта работа должна равняться изменению кинетической энергии вращения , где и 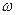– начальная и конечная угловые скорости вращения. Кинетическая энергия вращающихся тел используется в технике, например, при внезапном увеличении нагрузки машина не останавливается, а совершает работу за счет запаса кинетической энергии вращения маховика.