Средства обеспечения дисциплины 6 страница

6. Обобщите закон сохранения импульса для случая релятивистских движений.

7. В чем заключается постоянство скорости центра масс замкнутой системы?

8. На тележке стоят два бака, соединенные между собой в нижней части трубкой с краном. Один из баков наполнен водой. При открывании крана вода переливается в пустой бак. Будет ли при этом двигаться тележка? Когда она остановится? Трение между тележкой и землей не учитывать.

9. Зенитный снаряд разрывается на высоте h от земли на большое число осколков, имеющих одинаковую начальную скорость 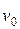и равные массы. Найдите расстояние между двумя осколками, лежащими на прямой, проходящей через центр инерции всей системы и образующей угол 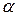с вертикалью, через время 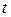после разрыва.

10. Почему удар молотком по тяжелой наковальне, положенной на грудь циркового артиста, оказывается для него безвредным, тогда как такой же удар прямо по телу артиста является гибельным?

11. Приведите примеры проявления закона сохранения импульса.

12. Что такое приведенная масса и в чем смысл введения этого понятия?

Лекция №6. Законы сохранения

Для замкнутой системы тел остаются постоянными три физические величины: энергия, импульс и момент импульса. Соответственно имеются три закона сохранения: закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса. Второй закон – закон сохранения импульса изучили в предыдущем разделе. Настоящий раздел посвящен рассмотрению остальных двух законов сохранения в механике.

1. Работа

Понятия работы и энергии широко используются в нашей повседневной жизни. Эти понятия тесно связаны друг с другом. Например, говорят об энергичном или работоспособном человеке, или говорят, что «очень устал, очень много работал или энергию затратил и т.д.». Греческое слово «энергия» означает «деятельность». Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Например, совершая работу при заводе часов, мы создаем запас энергии в пружине, за счет которого затем идут часы.

Пусть при перемещении материальной точки В по некоторой траектории на малый отрезок 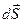на эту точку действует сила 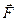, направление которой составляет угол 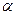с направлением перемещения (рис.6.1).

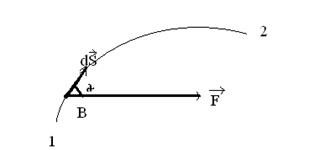
Рис.6.1

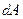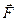Элементарной работой силы на малом перемещении 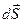называется произведение величины 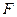этой силы на величину перемещения и на косинус угла 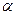между направлением силы и направлением перемещения:

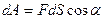(6.1)

Из определения (6.1) следуют следующие особенности элементарной работы.

1. Элементарная работа – это скалярное произведение силы на малое перемещение, т.е.

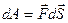(6.2)

Она может быть представлена в виде

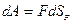, (6.3)

или 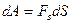, (6.4)

где 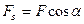– проекция силы на направление перемещения, – проекция перемещения на направление силы.

Последние формулы показывают, что перемещение тела обусловлено только касательной составляющей силы 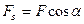, которую называют движущей силой. Причем, эта сила должна быть постоянной на элементарном перемещении 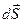. Поэтому элементарная работа равна произведению постоянной движущей силы на величину перемещения.

2. Работа – скалярная величина. Она может быть как положительной, так и отрицательной. При 0< 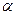<90° работа положительна – сила вызывает перемещение тела; при 90°< 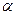<180° работа отрицательна – сила препятствует движению тела; при 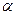=90° сила не совершает работы по перемещению тела. Если направления силы и перемещения совпадают ( 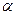= 0°), то

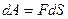(6.5)

3. Если материальная точка перемещается под действием нескольких сил, то совершаемая ими работа равна сумме работ всех этих сил.

4. Если работа совершается переменной силой, то следует разделить участок траектории на элементарные отрезки так, чтобы их можно было считать прямолинейным, и сложить элементарные работы, совершаемые движущей силой на каждом из отрезков этого участка:

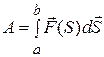, (6.6)

где аb – участок траектории.

Из формулы (6.6) вытекает, что полная работа, совершаемая материальной точкой под действием постоянной движущей силы по всей траектории, равна:

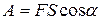(6.7)

5.Работа является количественным выражением действия силы или взаимодействия тел. Поэтому конечное выражение для вычисления работы определяется видом взаимодействия. Например, если на тело действует только сила тяжести, работа, совершаемая телом, равна: 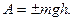Если тело поднимается вверх, то сила тяжести совершает отрицательную работу, если оно опускается вниз, то – положительную работу. Величина работы не зависит от формы траектории, по которой двигалось тело, а определяется лишь тем, насколько выше или ниже находится конечная точка участка траектории по сравнению с начальной.

Силы, работа которых не зависит от формы и длины пути (траектории), а зависит лишь от начального и конечного положения тела, на которое они действуют, называются консервативными. Из этого определения следует, что работа по любому замкнутому контуру для таких сил равна нулю:

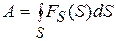=0 (6.8)

К ним относятся все центральные силы, т.е. силы всемирного тяготения (и силы тяжести), силы упругости и др. К неконсервативным силам относятся, например, сила трения скольжения, силы сопротивления движению тел.

Силы трения называют также диссипативными силами, поскольку при наличии в системе материальных точек взаимодействий, осуществляемых этими силами, происходит исчезновение механической энергии и превращение её в тепловую (диссипация – рассеяние, уничтожение).

6.В качестве единицы работы в СИ является джоуль (Дж), который равен работе, совершаемой силой 1 Н на пути 1 м; в СГС-системе – эрг, равный работе, совершаемой силой 1 дин на пути 1 см.

7.Работа, совершаемая в единицу времени, называется мощностью.

Мощность P определяется соотношением 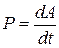, где 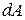– работа, совершаемая за время 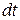. Подставив вместо 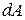выражение (6.2) и приняв во внимание определение скорости, получим .

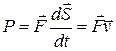Таким образом, мощность равна скалярному произведению силы на скорость точки приложения силы.

Единицей мощности является такая мощность, при которой за одну секунду совершается работа, равная одному джоулю. Эта единица называется ваттом (Вт).

2. Энергия и работа

Энергиейназывают физическую величину, являющуюся общей количественной мерой различных форм движения и существования материи, происходящих в результате совершения работы.

Таким образом, энергия является функцией состояния тела, например, движение тела приводит к изменению его энергии. Сам процесс изменения есть результат работы: .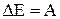

Катящийся шар, сталкиваясь с некоторым телом, перемещает его, т.е. совершает работу. Следовательно, катящийся шар обладает энергией. Кроме того, катящийся шар обладает энергией независимо от того, совершает он в данный момент работу или нет: энергия характеризует состояние системы, способность (возможность) системы к совершению работы при переходе из одного состояния в другое.

В физике в соответствии с различными физическими процессами и взаимодействиями различают механическую, тепловую, электромагнитную, ядерную и другие энергии.

Механическая энергия состоит из кинетической и потенциальной энергий.

3. Кинетическая энергия и работа

Пусть под действием некоторой силы 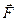тело (материальная точка) массой 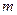совершает перемещение, изменив скорость от 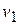до 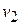, т.е. движется с ускорением . Напишем уравнение движения тела:

(6.9)

Учитывая определение ускорения материальной точки и умножив уравнение (6.9) на перемещение точки 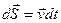, получим

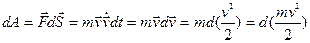(6.10)

Проинтегрировав соотношение 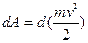с учетом изменения скорости тела, имеем .

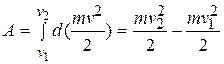Введем обозначение , которое называется кинетической энергией тела.

Итак, совершенная силой работа равна приращению кинетической энергии тела:

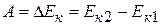(6.11)

В этом заключается и физический смысл работы.

Из определения следует, что:

- кинетическая энергия – это энергия движения;

- кинетическая энергия – скалярная величина;

- кинетическая энергия системы материальных точек равна сумме кинетических энергий всех точек, составляющих систему;

- измеряется в тех же единицах, что и работа.

4. Потенциальная энергия

Потенциальная энергия обусловлена характером взаимодействия между телами, их взаимным расположением. Поэтому вид формулы для потенциальной энергии зависит от конкретного вида взаимодействия тел.

Так, например, работа силы тяжести, необходимая для изменения положения тела относительно Земли, равна: 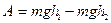, где 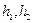– начальная и конечная высота ( 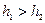) тела относительно Земли. Выражение 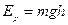называется потенциальной энергией силы тяжести. Эта работа равна изменению потенциальной энергии тела:

(6.12)

Положительная работа сил тяжести соответствует убыли потенциальной энергии. Наоборот, если бы тело поднималось над поверхностью Земли, приращение потенциальной энергии соответствовало бы отрицательной работе. Поэтому в общем случае следует записать: 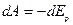. Так как 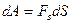, то и

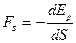(6.13)

Формула (6.13) показывает, что консервативная сила – сила тяжести – равна градиенту потенциальной энергии, взятому с обратным знаком:

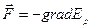(6.14)

Эта формула связывает между собой силу и соответствующую ей потенциальную энергию, что дает возможность вычислить потенциальную энергию в каждом конкретном случае вида взаимодействия тел.

Пример. Пусть задана сила всемирного тяготения 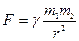. Так как 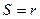, из формулы (6.13) найдем

.

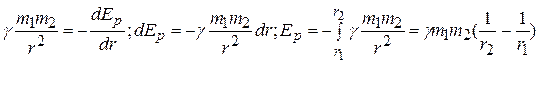Обычно за начальную конфигурацию системы, состоящую из двух материальных точек, взаимодействующих между собой силами всемирного тяготения, принимают расположение этих точек на бесконечно большом расстоянии друг от друга, где 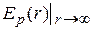=0. Тогда потенциальная энергия взаимодействия точек равна

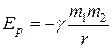(6.15)

Как и закон всемирного тяготения, эта формула верна не только для материальных точек, но и для любых сферически симметричных тел.

Физически знак минус обусловлен тем, что по мере самопроизвольного сближения тяготеющих тел их потенциальная энергия должна уменьшаться, переходя в кинетическую. Из формулы (6.15) следует, что максимальное значение потенциальной энергии тяготеющие тела будут иметь в том случае, когда они бесконечно удалены друг от друга.

Выше мы говорили о потенциальных и консервативных силах. Они тождественны лишь в случае стационарного силового поля, т.е. поля, остающегося постоянным во времени. Поле консервативных сил является частным случаем потенциального силового поля. Для нестационарного силового поля, т.е. поля, изменяющегося во времени, формула (6.14) не выполняется. Поэтому отождествлять потенциальные и консервативные силы нельзя.

5. Закон сохранения и превращения механической энергии

Рассмотрим систему, состоящую из двух материальных точек с массами 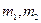. Пусть частицы взаимодействуют друг с другом с силами 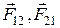, модули которых зависят только от расстояния между материальными точками . Такие силы являются консервативными. Предположим, что, кроме консервативных сил, на каждую точку действуют внешняя консервативная сила 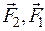и внешняя неконсервативная сила 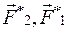. Тогда уравнение движения каждой точки имеет вид:

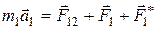, (6.16)

Умножив уравнения (6.16) на соответствующие перемещения 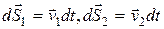, учитывая определение ускорения материальной точки и сложив вместе полученные уравнения, имеем

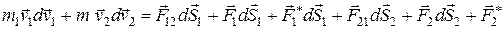(6.17)

Левая часть представляет собой приращение кинетической энергии системы:

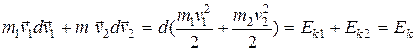(6.18)

Первый и четвертый члены правой части равны убыли потенциального взаимодействия частиц: 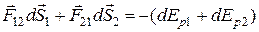(6.19)

Второй и пятый члены правой части равны убыли потенциальной энергии во внешнем поле консервативных сил: .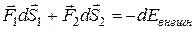

Остальные члены представляют собой работу неконсервативных внешних сил:

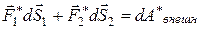(6.20)

Приняв во внимание (6.18)-(6.20), представим соотношение (6.17) следующим образом:

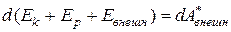(6.21)

Величина 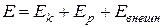есть полная механическая энергия системы. Если внешние неконсервативные силы отсутствуют, правая часть формулы (6.20) будет равна нулю и, следовательно, полная энергия системы остается постоянной:

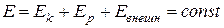(6.22)

Таким образом, мы пришли к выводу, что полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной. В этом и заключается закон сохранения механической энергии.

Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, соотношение (6.22) имеет вид

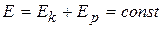(6.23)

В этом случае закон сохранения механической энергии формулируется следующим образом: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной.

Если в замкнутой системе, кроме консервативных, действуют также неконсервативные силы, например силы трения, то полная механическая энергия системы не сохраняется. Рассматривая неконсервативные силы как внешние, можно в соответствии с (6.21) написать

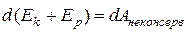(6.24)

Пример. Основными запасниками механической энергии во время бега и других циклических движений являются сухожилия. Каждый из нас может убедиться, что механическая энергия действительно запасается в наших ногах, как в пружинах. Сильно сгибая ноги в этом можно убедиться. Мы сразу заметим, что подниматься гораздо легче, если выпрямить ноги сразу, чем если задерживаться на секунду. Это можно объяснить тем, что при сгибании колен часть мышц напряжена, контролируя движение вниз, и их сухожилия растянуты. Если перед подъемом сухожилиям не дать возможность укоротиться, запасенная в них потенциальная энергия перейдет в кинетическую. В этом случае выполняется закон сохранения механической энергии для замкнутой системы тел. В противном случае между мышцами появляются неконсервативные силы, что проявляется в нагреве тела: полная механическая энергия системы не сохраняется, часть механической энергии переходит в тепловую.

Свойства сухожилий более или менее одинаковы у всех животных. Однако конечности копытных, например, овец и лошадей, наиболее приспособлены для хранения механической энергии. Некоторые мышцы в нижних частях ног этих животных состоят практически целиком из одних сухожилий. Самым выразительным примером такого использования сухожилий могут служить нижние конечности верблюда. В ноге человека самым мощным является ахиллово сухожилие, на которое при беге может действовать растягивающая сила до 4000 Н.

6. Соударение двух тел

Ударом называется кратковременное столкновение соударяющихся тел. Соударяющиеся тела можно считать замкнутой системой, так как возникающие при кратковременном ударе внутренние силы системы во много раз превосходят внешние. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает. Кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела либо покоятся, либо движутся с одинаковой скоростью. При абсолютно неупругом ударе выполняется только закон сохранения импульса.

Пусть массы соударяющихся частиц (материальных частиц) равны 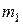и 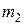, а скорости до удара – 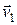и 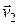, а после соударения – . По закону сохранения импульса .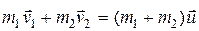

Отсюда имеем 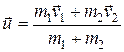(6.25)

Можно найти изменение кинетической энергии шаров, т.е. ту часть, которая перешла во внутреннюю энергию:

.

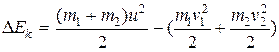Подставляя сюда (6.25), получим 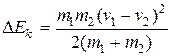. Эта энергия переходит в тепловую энергию.

Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, модуль и направление которых определяются двумя условиями – сохранением полной энергии и сохранением полного импульса системы тел.

В качестве примера рассмотрим абсолютно упругий центральный удар двух однородных шаров. Удар называетсяцентральным, если шары до удара движутся вдоль прямой, проходящей через их центры.

Обозначим скорости шаров после удара через 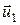и 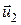. Напишем законы сохранения энергии и импульса:

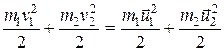, (6.26)

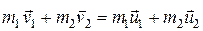(6.27)

Решая эту систему уравнений, находим скорости шаров после удара:

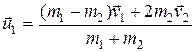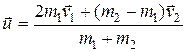, (6.28)

Отметим, что скорости шаров после абсолютно упругого удара не могут быть одинаковыми.

7. Момент силы относительно неподвижного центра

Повседневный опыт показывает, что при вращении какого-либо тела с помощью рычага существенным оказывается не только модуль силы, но и длина рычага.Для описания динамики вращения такого тела необходимо ввести понятие момента силы.При этом надо различать понятия момента силыотносительно точки и относительно оси. Это разные понятия.

M     O F r a A Рис.6.2. Момент силы относительно точки

Момент силы относительно точки сам есть вектор. Момент того же вектора относительно оси есть проекция на эту ось его момента относительно точки, лежащей на той же оси. Таким образом, момент вектора относительно оси уже не является вектором. Рассмотрим момент силы относительно точки.

Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы или вектора импульса. Ее называют началом или полюсом. Обозначим радиус-вектор 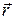, проведенный из этой точки к точке приложения силы 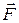(Рис.6.2). Моментом силы 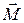относительно неподвижной точки О называется векторное произведение радиуса-вектора 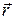, проведенного из точки О к точке А, и вектора силы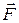

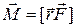(6.29)

Из этого определения следует, что момент 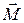не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.

Если 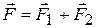, то на основании известного свойства векторного произведения можно написать

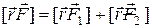(6.30)

Это значит, что момент равнодействующей двух или нескольких сил относительно некоторого начала или произвольной точки равен геометрической сумме моментов составляющих сил относительно того же начала.

Как следует из (6.29), модуль момента силы 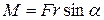, где есть плечо силы. Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила.

Направлен вектор 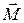перпендикулярно к плоскости, в которой лежат сила и точка О, причемнаправление вектора 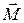определяется правилом правого буравчика: поворот головки винта или шурупа с правой нарезкой в направлении силы вызвал бы перемещение винта в направлении вектора .

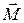8. Момент импульса относительно неподвижного центра

По аналогии с моментом силы, моментом импульса материальной точки (частицы) относительно точки О называется векторная величина

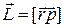(6.31)

В этой формуле – импульс частицы. Модуль момента импульса

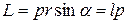, (6.32)

где называется плечом импульса (рис.6.3).

Таким образом, момент импульса равен произведению плеча импульса на модуль вектора импульса.

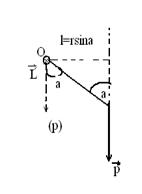
Рис. 6.3. Направление и модуль импульса со временем изменяются. При этом изменяются и плечо, а также модуль и направление вектора . Вектор 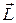изображен в виде кружка с крестиком внутри. Следовательно, он направлен “от нас”.

Частица обладает моментом импульса независимо от формы траектории, по которой она движется. Рассмотрим два частных случая.

1. Частица движется вдоль прямолинейной траектории (рис.6.4). Модуль момента импульса

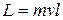(6.33)

может изменяться только за счет изменения модуля скорости.

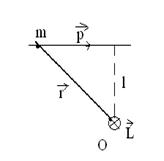
Рис.6.4

2. Частица движется по окружности радиуса 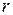(рис.6.5). Модуль момента импульса относительно центра окружности равен и так же, как и в предыдущем случае, может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора 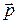, направление вектора 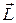остается постоянным.