Средства обеспечения дисциплины 3 страница

Пусть движение происходит равноускоренно вдоль оси Ох, т.е. движение равноускоренное и прямолинейное. Тогда из первого уравнения (3.15) имеем:

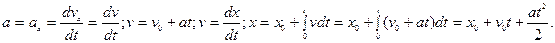
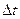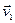
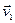
Рассмотрим подробнее, как меняется скорость при криволинейном движении. Пусть материальная точка за некоторый промежуток времени перемещается из положения А в положение В с изменением скорости от до . Перенесем вектор параллельно самому себе так, чтобы его начало совпало с точкой А. Соединим концы векторов и . Тогда приращение векторов скорости равно 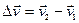. Отложим на векторе 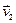вектор, равный вектору 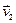. Следовательно, вектор 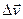можно рассматривать как сумму двух составляющих: как показано на рисунке, обозначим их 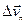и 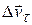, т.е. 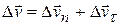. Тогда среднее ускорение равно .

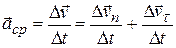Используя (3.11), из последнего выражения получим:

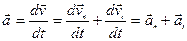, (3.17)

где 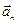и 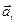– соответственно нормальное и тангенциальное ускорения. Причем в пределе направления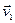 и 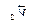практически совпадают, следовательно, вектор 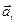направлен так же, как и вектор 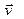по касательной в каждой точке траектории, а его значение определяют изменения величины (модуля) скорости:

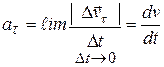(3.18)

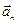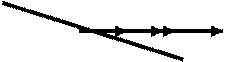
Нормальная составляющая ускорения при этом окажется перпендикулярной вектору скорости 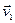, направленному перпендикулярно касательной к траектории, и показывать изменение направления скорости (рис. 3.4).

V

ατ

α

αn

Рис.3.4

Величина (модуль) полного ускорения при его разложении на нормальную и тангенциальную составляющие равна:

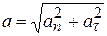(3.19)

3.Ускорение при движении материальной точки по окружности

Пусть точка движется равномерно по окружности радиуса 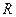с постоянной по величине во времени скоростью. Движение точки является криволинейным. Поэтому при равномерном движении точки по окружности должно существовать нормальное ускорение, обуславливающее изменение направления скорости.

Если материальная точка за некоторый промежуток времени 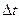перемещается из положения А в положение В с изменением скорости от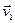 до 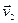, то приращение скорости за это время равно 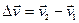(рис. 3.5).

A v₁

∆S =∆r

R

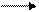v₁

О B D

R∆v

C v₂

Рис. 3.5.

Перенесем вектор 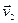параллельно самому себе так, чтобы его начало совпало с точкой В. Рассмотрим треугольники АОВ и СВД. Они подобны, так как ÐАОВ =ÐСВД и эти треугольники являются равнобедренными (ОА=ОВ=R , ВС=ВД= 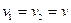. Поэтому составим пропорцию: . Отсюда 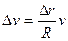. Найдем ускорение точки. Разделим обе части последнего равенства на 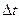и перейдем к пределу при 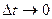. Таким образом,

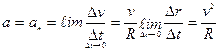(3.20)

Итак, при движении точки по окружности её нормальное ускорение зависит от скорости точки и от радиуса окружности. Оно направлено по радиусу к центру окружности и поэтому его называют центростремительным ускорением.

Для любого положения движущейся точки можно написать 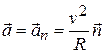, где 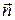– единичный вектор нормали к круговой траектории движущейся точки, направленный к центру окружности.

Если точка движется по окружности неравномерно, то вектор скорости меняется и по величине, и по направлению. В этом случае существуют и тангенциальное и нормальное ускорения. Следовательно, полное ускорение направлено под углом к радиусу. Так как нормальное ускорение связано с изменением только направления вектора скорости, то и в случае неравномерного движения по окружности оно выражается формулой (3.20).

Рассмотрим движение точки по произвольной криволинейной траектории. Из геометрии известно, что небольшой её участок (рис.3.6) всегда можно заменить дугой окружности некоторого радиуса 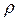. Такая окружность называется кругом кривизны траектории в данной точке. Радиус его называется радиусом кривизны, величина, обратная ему, – кривизной.

ρ

ρ

ρ

Рис. 3.6.

При этом для нормального ускорения формула (3.20) сохраняется, но под радиусом окружности следует подразумевать радиус кривизны траектории. Таким образом, величина вектора полного ускорения при криволинейном движении определяется выражением:

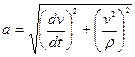(3.27)

4. Кинематика вращательного движения материальной точки

Введенные выше кинематические законы движения достаточны для описания любого вида движения материальной точки. Однако в случае вращательного движения удобнее пользоваться понятиями угловой скорости и углового ускорения.

Рассмотрим простейший случай движения материальной точки по окружности радиуса R . Выберем на окружности некоторую точку О^! в качестве начала отсчета и проведем в неё из центра окружности радиус ОО^! (рис.3.7).

O^!

А

R

А^!

φ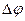

O

Рис. 3.7.

Положение точки А, движущейся на окружности, в некоторый момент времени можно определить при помощи угла 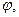который составляет радиус ОА, проведенный к точке с начальным радиусом ОО₁. Тогда закон движения точки может быть выражен функцией: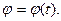

Пусть через некоторый промежуток времени 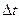точка оказалась в положении А₁, и угол 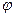при этом изменился на величину 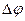. Быстрота изменения угла 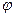с течением времени определяется как предел, к которому стремится отношение 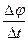, если промежуток времени 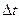стремится к нулю, т.е.

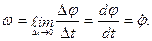(3.28)

Единицей измерения угловой скорости является радиан в секунду (рад/с или 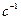). Рад/с – угловая скорость равномерно вращающегося тела, при которой за время 1 с совершается поворот тела относительно оси на угол 1 рад.

Угловым ускорением называют величину, характеризующую быстроту изменения угловой скорости:

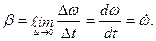(3.29)

С учетом (3.28) также имеем:

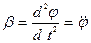(3.30)

При малом угле поворота связь между линейным и угловым перемещением 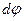можно выразить соотношением:

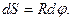
Исходя из этого выражения, легко устанавливается связь между линейной скоростью v (скорость точки вдоль траектории) и угловой скоростью 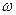. Для этого достаточно разделить последнее выражение на :

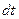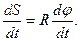
Отсюда, в силу формул (3.3) и (3.28), имеем

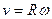(3.31)

Аналогично получим связь тангенциального ускорения (а не нормального!) с угловым:

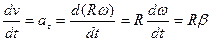(3.32)

А для определения величины нормального ускорения воспользуемся формулой : 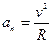. Тогда .

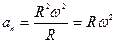Заметим, что при движении материальной точки по окружности, т.е. при вращательном движении, радиус-вектор 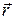направлен от центра по радиусу окружности 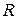, формулу для центростремительного (или нормального) ускорения можно записать в векторной форме .

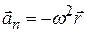Знак минус указывает на то, что направления векторов 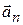и 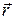взаимно противоположны, т.е. ускорение 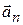направлено к центру круговой траектории, по которой вращается материальная точка.

Время одного полного оборота называется периодом Т. Тогда угловая скорость 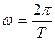, т.е. 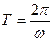, частота n .

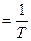Контрольные вопросы

1. Дайте определение средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения. Каковы их направления?

2. Что характеризуют тангенциальная и нормальная составляющие ускорения? Каковы их модули?

3. Возможны ли движения, при которых отсутствуют нормальное и тангенциальное ускорения? Приведите примеры.

4. Что называется угловой скоростью и угловым ускорением?

5. Какова связь между линейными и угловыми величинами?

6. Выведите уравнения движения и формулу скорости для равноускоренного и равнозамедленного движений (с начальной и без начальной скорости).

7. Постройте графики скорости равномерного, равноускоренного и равнозамедленного движений.

8. Как движется тело, брошенное вертикально вверх?

9. Сформулируйте принцип независимости движений.

10. Дан вектор скорости тела в некоторый момент времени. Можно ли определить ускорение тела в этот момент?

11. Между точками А и В движется по прямой тело таким образом, что, выходя из точки А с нулевой начальной скоростью, оно должно иметь в точке В скорость, равную рулю. При этом тело может двигаться равномерно или с постоянным по модулю ускорением а. Каким должен быть характер движения, чтобы время его было минимальным?

12. Определите, на какую величину путь, пройденный свободно падающим телом в n-ую секунду, больше пути, пройденного в предыдущую секунду?

13. С некоторой высоты падает коробка, в центре которой находится металлический шарик, не соприкасающийся с ее стенками. Определите движение шарика относительно стенки коробки во время падения. Сопротивление воздуха не учитывать.

14. Как изменяются время и дальность полета тела, брошенного горизонтально, при увеличении высоты его подъема в четыре раза? Скорость бросания при этом не изменяется.

15. Под каким углом к горизонту надо бросить тело, чтобы наибольшая высота подъема была равна дальности полета? Считать, что на тело действует попутный ветер, сообщающий ему горизонтальное ускорение.

16. Под некоторым углом к горизонту из шланга бьет струя воды. Почему восходящая ветвь струи сплошная, а нисходящая рассыпается на отдельные части?

Лекция №4. Динамика материальной точки

Динамика– раздел механики, в котором изучаются законы движения тел в связи с вызывающими его физическими причинами. Основные положения динамики точки были сформулированы И. Ньютоном в его «Математических началах натуральной философии» в 80-х годах 17 века в виде трех законов движения. Законы Ньютона возникли в результате обобщения большого количества наблюдений и экспериментов. Правильность их подтверждается соответствием с опытом тех следствий, которые из них вытекают.

Первый шаг в понимании движения был сделан Г.Галилеем, когда он открыл впервые свой принцип инерции: тело, предоставленное самому себе, если на него не действует никакая сила, сохраняет свое прямолинейное движение с постоянной скоростью, как двигалось до этого, или остается в покое, если оно до этого покоилось. Конечно, в природе такого не бывает. Например, шарик, катящийся по поверхности стола, останавливается за счет силы трения.

Естественным является вопрос: как движется тело, почему оно движется так, а не иначе, какие причины вызывают или изменяют это движение. На эти вопросы ответ дал И.Ньютон, сформулировав три закона.

1. Первый закон Ньютона

Этот закон Ньютон сформулировал следующим образом:

Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не выведет его из этого состояния.

Существуют такие системы отсчета, в которых всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Поэтому и называется первый закон законом инерции. Инерциальных систем отсчета множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, т.е. поступательно с постоянной скоростью является инерциальной. Чтобы убедиться в этом, рассмотрим движение материальной точки относительно систем отсчета К и 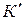(рис.4.1) . Допустим, что система 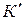движется относительно системы К поступательно с постоянной скоростью 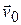. Как видно из рисунка, между радиус-векторами имеется соотношение

.

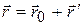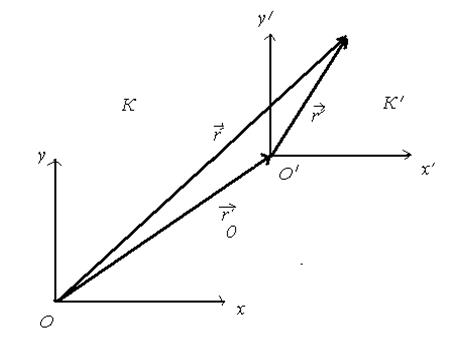
Рис. 4.1.

Продифференцировав его по времени, найдем, что 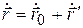, т.е. .

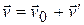Если на материальную точку не действуют никакие тела и система инерциальна, то скорость материальной точки в этой системе будет постоянной. Из последней формулы следует, что скорость материальной точки 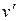в системе 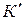также оказывается постоянной. Это означает, что система 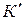также инерциальна.

Установить, является ли данная система инерциальной или нет, можно опытным путем. Например, опыт показывает, что с большой степенью точности систему отсчета, связанную с Землей (геоцентрическая система отсчета) при изучении явлений, происходящих на Земле, можно считать инерциальной.

С гораздо большей точностью можно считать инерциальной систему отсчета, в которой начало координат совмещено с Центром Солнца, а координатные оси направлены на три неподвижные звезды, сохраняющие с известной точностью неизменное положение на небесном своде (гелиоцентрическая система отсчета). Она является инерциальной при описании явлений, происходящих в солнечной системе, а не в галактике.

Очевидно, первый закон является приближенным законом.

Во-первых, нет и не может быть ни с чем не взаимодействующих тел. Чем меньше это взаимодействие, тем точнее выполняется первый закон. Например, если ударить ногой по мячу, то он после падения по траве продвинется значительно меньше, чем по асфальту, по которому он катится десятки метров, не снижая своей скорости. Это расстояние зависит, во-первых, от силы удара ноги, и, во-вторых, от шероховатости поверхности. Лишь считая, что поверхность идеально гладкая и воздействие на тело других тел в вертикальном направлении отсутствует, можно сделать вывод о справедливости первого закона Ньютона.

Во-вторых, зависит от выбора тела отсчета. Например, на перроне лежит камень. Он находится в покое относительно перрона, т.е. инерциальной системы отсчета. Однако для наблюдателя, которое смотрит на камень из окна трогающегося поезда, камень движется ускоренно, хотя ясно, что никаких новых воздействий на камень при трогании с места не появилось. Ускоренное движение камня относительно поезда нельзя объяснить воздействием какого-либо тела. В этом случае первый закон не выполняется относительно системы отсчета, связанной с поездом.

2. Масса

Опыт показывает, что при одинаковом воздействии различные тела по-разному изменяют скорость и получают различные ускорения. Это свойство тел влиять на величину собственного ускорения называется инертностью тел. Следовательно, величина ускорения, приобретаемого телом, зависит от некоторого собственного свойства тела. Это свойство тела характеризуют физической величиной, называемой массой.

Таким образом, масса – мера инертности тела. Под инертностью понимают неподатливость тела действию сил, т.е. свойство тела противиться изменению скорости под воздействием силы. В дальнейшем увидим также, что масса характеризует и гравитационные свойства тел и их энергосодержание.

Масса – скалярная величина. Следовательно, массы тел складываются алгебраически.

Масса составного тела равна сумме масс составляющих тел. Это свойство называется аддитивностью массы.

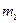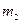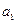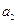Массы и двух тел обратно пропорциональны ускорениям и , которые эти тела приобретают под действием одной и той же силы, т.е. .

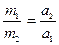Поэтому масса тел определяется путем сравнения с массой некоторого произвольно выбранного эталонного тела. По международному соглашению таким эталоном является платино-иридиевый цилиндр, хранящийся в Париже и называемый килограммом массы (кг). Эта масса принята за единицу массы – 1 кг. Тысячная доля кг называется граммом массы (г). С высокой степенью точности масса 1 см³ дистиллированной воды при 4 ⁰С равна 1 г.

При малых скоростях, т.е. таких, с которыми имеют дело в классической механике, масса – постоянная величина. Однако для тел, движущихся со скоростью, близкой к скорости света, масса зависит от скорости:

,

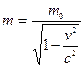где 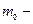масса тела при 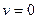(масса покоя), 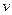– скорость тела, 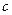– скорость света, равная 3· 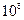м/с.

Эта формула была получена А.Эйнштейном в 1905 г. Она показывает, что масса возрастает с увеличением скорости. В современных ускорителях электроны разгоняются до таких скоростей, при которых их масса возрастает в тысячи раз. Последняя формула также показывает, что тело не может иметь скорость, превышающую скорость света (в пустоте). По мере увеличения скорости тела растет и его масса, а ускорение уменьшается.

3. Сила

Согласно первому закону Ньютона, если на тело действуют другие тела, то состояние движения тела изменяется, т.е. изменяется его скорость и появляется ускорение. Количественной мерой воздействия на данное тело со стороны другого тела является сила.

Из определения следует, что понятие сила относится к двум телам. Если имеется сила, всегда можно указать тело, на которое она действует, и тело, со стороны которого она действует.

Общие свойства сил устанавливаются при рассмотрении особенностей влияния воздействия на ускорение. Они заключаются в следующем.

1. Так как ускорение является вектором, то и сила, вызывающая ускорение тела, является вектором, т.е. характеризуется и величиной, и направлением. Если силу обозначить через 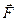, то:

- вектор силы можно представить в ви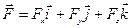де , где 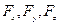– составляющие вектора силы по координатным осям;

- величина силы равна

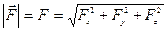(4.1)

2. Ускорение тела, подвергающегося воздействию, зависит:

- от свойств этого тела (например, деревянный шарик катится мимо магнита равномерно по прямой, а стальной шарик – по кривой траектории);

- от свойств тела, оказывающего воздействие (например, стальной шар катится по кривой траектории вблизи магнита, а вблизи деревянного магнита – прямолинейно);

- от расстояния между телами, подвергающимися и оказывающими воздействие (чем ближе стальной шар подходит к магниту, тем больше искривляется траектория шарика);

- от относительной скорости взаимодействующих тел.

Сила, являясь характеристикой взаимодействия тел, также может зависеть от указанных особенностей.

Сила проявляется и в деформации тел. Например, груз, висящий на проволоке, растягивает её. По величине деформации можно определить величину силы. На этом основано измерение силы пружинным динамометром.

4. Второй закон Ньютона

Второй закон Ньютона гласит: ускорение 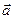, приобретаемое телом под действием силы 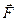, направлено так же, как и сила, а по величине пропорционально силе и обратно пропорционально массе 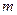тела: ~ .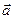

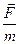Из последнего соотношения следует, что 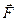~ 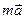. Вводя коэффициент пропорциональности к, получим

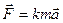(4.2)

Коэффициент 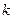зависит от выбора системы единиц. Во всех используемых в настоящее время системах единиц полагается 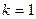. Таким образом, из (4.2) имеем

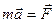(4.3)

Выражение (4.3) и представляет собой одну из формулировок второго закона Ньютона: произведение массы материальной точки на ее ускорение равно силе, действующей на материальную частицу.