Время лечения больных пневмонией в стационаре
| Количество дней (х) | Количество больных (f) | x f | d = x - 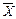
| d2 | d2 f |
| -3 | |||||
| -2 | |||||
| -1 | |||||
| n=48 | ∑=110 |

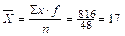 дней
дней 
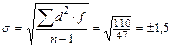 дня
дня
Последовательность расчета среднего квадратического отклонения:
1. Определяем среднее арифметическое ( 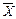 ).
).
2. Находим отклонение вариантов от среднего арифметического (d).
3. Возводим отклонения (d) в квадрат (для избежания больших значений и увеличения значений крайних отклонений).
4. Перемножаем квадраты отклонений на соответствующей частоте - (d2 f ) и определяем их сумму.
5. Определяем среднее квадратическое отклонение по приведенной формуле.
Для нашего примера: σ = ±1,5 дней.
Среднее квадратическое отклонение всегда определяют в тех именных числах, представление конкретными измеряемыми вариантами и средним. Оно характеризует абсолютную меру вариации - чем более непостоянный, рассеянный ряд, тем среднее квадратическое отклонение будет больше. Чем больше варьируют индивидуальные значения вариантов, тем менее точно характеризуется вариационный ряд с помощью среднего арифметического.
Практическая значимость среднего квадратического отклонения (сигмы) базируется на теории нормального распределения вариантов, согласно с которым их отклонения от среднего значения в ту или другую сторону встречаются равнозначно. Преобладающее большинство явлений при практическом анализе медико-биологических данных имеют нормальное распределение. Из теории статистики известно, что в нормальном вариационном ряду находится шесть средних квадратичных отклонений - равномерно по три с каждой стороны от среднего.
Исходя, из значений среднего арифметического 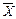 и среднего квадратического отклонения (σ) при симметричном ряде распределения можно с определенной степенью вероятности утверждать, что достоверное число вариантов будет находиться в определенных границах. Согласно с теорией математической статистики, что доказано на больших числах наблюдений, в границах (
и среднего квадратического отклонения (σ) при симметричном ряде распределения можно с определенной степенью вероятности утверждать, что достоверное число вариантов будет находиться в определенных границах. Согласно с теорией математической статистики, что доказано на больших числах наблюдений, в границах ( 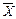 ±1 σ) будут иметь место не менее 68,3 % всех вариантов данной совокупности. В границах (
±1 σ) будут иметь место не менее 68,3 % всех вариантов данной совокупности. В границах ( 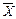 ±2 σ)будут распределены около 95,5 % всех вариантов. Практически весь вариационный ряд - 99,7 % вариантов находится в диапазоне (
±2 σ)будут распределены около 95,5 % всех вариантов. Практически весь вариационный ряд - 99,7 % вариантов находится в диапазоне ( 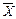 ±3 σ). Отдельные варианты - до 0,3 % исследований совокупности могут не отвечать общему характеру распределения и выпадать из него вследствие достаточно низкого или высокого уровня (" выскакивающие " варианты).
±3 σ). Отдельные варианты - до 0,3 % исследований совокупности могут не отвечать общему характеру распределения и выпадать из него вследствие достаточно низкого или высокого уровня (" выскакивающие " варианты).
Закономерностями распределения частот вариационного ряда можно воспользоваться при решении практических задач. Для приведенного выше примера плановая, предоперационная, средняя продолжительность госпитализации в больнице №1 составляет (3,1 ±0,3) дня. Анализ 200 случаев лечения позволяет сделать выводы: около 68,3 % больных (136 человек) имеют продолжительность предоперационного периода в среднем 2,8 -3,4 дня ( 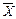 ±1 σ). У 95,5 % больных (округленно 195 пациентов) от становится 2,5 - 3,7 дней (
±1 σ). У 95,5 % больных (округленно 195 пациентов) от становится 2,5 - 3,7 дней ( 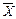 ±2 σ). Интервал 2,2 -4,0 дней (
±2 σ). Интервал 2,2 -4,0 дней ( 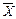 ±3 σ) описывает продолжительность предоперационного периода практически для всех обследуемых больных.
±3 σ) описывает продолжительность предоперационного периода практически для всех обследуемых больных.
Обобщение представленного материала позволяет сделать вывод о возможности использования среднего квадратического отклонения:
· Для определения амплитуды ряда;
· Обновления граничных его значений;
· Определения вероятного числа наблюдений в определенных интервалах.
Приведенные критерии распределения признаков ("сигмальная оценка") используют для индивидуальной оценки показателей физического развития, определения норм клинических и физиологических параметров. Интервал оценки показателей в границах ( 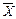 ±1 σ) в большинстве случаях определяет их средний уровень; в границах (
±1 σ) в большинстве случаях определяет их средний уровень; в границах ( 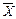 ±2 σ) (
±2 σ) ( 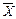 ±1 σ) - выше или ниже среднего; в границах (
±1 σ) - выше или ниже среднего; в границах ( 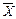 ±2 σ) - очень высокий, или очень низкий уровень показателей.
±2 σ) - очень высокий, или очень низкий уровень показателей.
Оценка среднего квадратического отклонения зависит не только от степени вариации признаков, а и от абсолютного уровня вариантов и среднего. Поэтому повсеместно сравнивать средние квадратические отклонения вариационных рядов с разными уровнями и единицами измерения, характеризующими неоднородные явления (длина в см, вес в кг ), нельзя. Для возможности такого сопоставления необходимо определить для каждого ряда отношение среднего квадратического отклонения к средней арифметической в процентах, то есть определить коэффициент вариации, изменчивости (С). Он является относительной мерой вариабельности, которая выражается в именованных числах, критерием надежности средней величины и определяется по формуле:
 |
С=( σ/
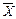 ) 100 %
) 100 %
Чем выше коэффициент вариации, тем больше вариабельность данного признака.
Например, определили, что после дозированной нагрузки средняя частота пульса у обследуемых составляла 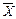 = 90 уд. / мин., σ = 8 уд. / мин., а артериальное давление
= 90 уд. / мин., σ = 8 уд. / мин., а артериальное давление 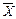 =135 мм рт.ст., σ =7 мм рт.ст..
=135 мм рт.ст., σ =7 мм рт.ст..
Коэффициент вариации для первого (по частоте пульса) ряда:
С= (8/90) 100 = 8,89 %
Коэффициент вариации для другого (по артериальному давлению) рада:
С=(7/135) 100 = 5,18 %
Для данного примера артериальное давление более устойчивый признак, чем частота пульса, Таким образом, коэффициент вариации дает более точку оценку изменчивости явлений и определяет наибольшую (наименьшую) вариабельность их признаков.
Ориентировочными критериями оценки вариабельности по его коэффициентам можно считать: низкий уровень - до 10 %.; средний уровень - 10-20 %, высокий уровень - выше 20 %. Высокий уровень коэффициента свидетельствует о невысокой точности обобщающей характеристики средней величины, одним из путей повышения которой является увеличения числа наблюдений.
Дата добавления: 2015-08-04; просмотров: 709;
