Распределение мальчиков 7 лет по росту
| Рост (х) | Количество мальчиков (f) |
| 125,0 - 126,9 127,0 - 128,9 129,0 - 130,9 131,0 - 132,9 | |
| Всего | n=28 |
В приведенном примере (табл.1) интервалы являются закрытыми - каждый интервал имеет верхнюю и нижнюю границу. В практике встречаются открытые интервалы (возраст 60 лет и старше, рост 120 см и больше и т.д.). При анализе ширину открытого интервала, обычно, считают равной ширине смежного с ним интервала.
Сгруппированный интервальный вариационный ряд получают путем объединения вариантов в группы. При этом необходимо помнить, что: а) размер вариационных групп должен зависеть от природы явления; б) точно определить одинаковые интервалы; в) границы вариационных групп не должны повторяться.
Все вариационные ряды по качественным характеристикам распределяются на дискретные (прерывные), в которых варианты могут быть представлены только целыми числами или получены в результате подсчетов (распределение по частоте пульса, число койко-дней, посещений-вызовов) и непрерывные, где варианты могут быть представлены как целыми, так и дробными числами, или являются результатом обмеров (табл.1). Клинические параметры являются чаще всего примером непрерывных вариантов.
При использовании ЭВМ для обработки статистических данных группирование проводят по стандартным процедурам. Одной из них есть формула Стерджеса для определения оптимального числа групп:
n=1+3,322 * lg N
где n - число групп;
N - число единиц наблюдения.
Использование данной формулы целесообразно для большого числа наблюдений.
Другим вариантом, более гибким с практической точки зрения, является метод определения амплитуды ряда. Для определения вопросов о числе групп необходимо представить статистическую совокупность в виде рангового ряда, то есть расположить ее единицы в определенном порядке. При численности совокупности меньше 100 единиц не целесообразно планировать более 10 групп.
Разница между максимальным и минимальным значениям вариантов называется размахом или амплитудой (xmax-xmin).
Этапы составления интервального вариационного ряда таковы:
· Определение амплитуды ряда;
· определение числа групп;
· Определение величины интервала.
Расчет средних величин базируется на значениях вариантов. Если вариант представлен в виде интервала , за величину ее в каждом из них принимают центральный вариант, то есть середину интервала. Для дискретного ряда центральный вариант определяется как полсуммы одного интервала. Для непрерывного ряда (табл.1) ею является полсуммы начальных значений двух соседних интервалов:
(125,0 + 127,0 ) : 2 = 126 см.
Общую характеристику вариационного ряда проводят с помощью следующих параметров: средней арифметической ( 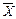 ), среднего квадратического отклонения ( σ ) , средней ошибки средней величины ( m ), коэффициента вариации ( С ), амплитуды (xmax-xmin).
), среднего квадратического отклонения ( σ ) , средней ошибки средней величины ( m ), коэффициента вариации ( С ), амплитуды (xmax-xmin).
Кроме выше указанного, в некоторых случаях для характеристики ряда целесообразно определять также моду и медиану.
Мода - это вариант, который имеет наибольшую частоту. Моду используют в тех случаях, когда необходимо дать характеристику признака, который наиболее часто встречается в исследуемой совокупности. Ее используют только в больших совокупностях.
Медианой в статистике называется вариант, который занимает среднее (центральное) положение в вариационном ряду. Медиана разделяет ряд наполовину - по обе стороны от него находится одинаковое количество единиц совокупности.
Среднее арифметическое - наиболее распространенный по частоте использования вид средних величин. Оно может быть простым или рассчитанным. Для простого вариационного ряда, в котором каждый вариант повторяется один раз, определяется простое среднее арифметическое, которое рассчитывается как отношение суммы значений вариантов к общему числу наблюдений.
Х= (∑х)/ n
где х -значения отдельных вариантов;
n - общее число наблюдений.
Для примера за частотой пульса, приведенного выше, определим
∑ 65+68+68+68+70+70+72+72+74+75+75

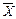 = = 70,5 (уд. мин) .
= = 70,5 (уд. мин) .
Для сгруппированного вариационного ряда определяется расчетное среднее арифметическое. Таким образом:
∑x f ∑ 65+68+68+68+70+70+72+72+74+75+75


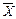 = = = 70,5 (уд. мин) .
= = = 70,5 (уд. мин) .
n 12
Частота, с которой встречается каждый вариант, называется "вес" варианта, а среднее арифметическое является рассчитанным, потому что варианты берут участие в общей сумме не одноразово, а как бы рассчитаны по числу соответствующих частот.
При определении среднего арифметического для сгруппированного интервального вариационного ряда: 1) определяют середину интервала, как сказано выше; 2) определяют произведение (результат) каждого центрального варианта на соответствующую для него частоту; 3) сумму произведений делят на число наблюдений.
Важнейшие свойства среднего арифметического:
· Произведение среднего на сумму частот всегда равно сумме произведений вариантов на частоту;
· Если от каждого варианта отнять произвольное число, то новое среднее уменьшится на то же число;
· Если для каждого варианта прибавить произвольное число, то среднее увеличится на то же число. Второе и третье свойства среднего арифметического показывают, что при уменьшении или увеличении вариантов на одно и то же число уменьшается или увеличивается уровень признака на то же число.
· Если каждый вариант разделить на произвольное число, то среднее арифметическое уменьшается в столько же раз.
· Если каждый вариант умножить на произвольное число, то среднее арифметическое увеличивается в столько же раз.
· Если все частоты (веса) разделить или умножить на любое число, то среднее арифметическое вследствие этого не изменится - если мы увеличиваем или уменьшаем равнозначно частоты всех вариантов, мы не изменяем вес каждого отдельного варианта ряда.
· Сумма отклонений вариантов от средней арифметической величины всегда равна 0. Это означает, что относительно среднего арифметического взаимно погашается отклонения вариантов в ту или другую сторону.
· Общие свойства можно использовать, чтоб облегчить технику определения среднего арифметического вариационного ряда.
Средняя гармоническая рассчитывается в тех случаях, когда известными являются данные о числителе при отсутствии таких о знаменателе. Например, необходимо определить среднее время, затраченное на прием одного больного, когда известно, что 5 врачей вели прием на протяжении 8 часов. Каждый из них затратил в среднем на прием одного больного соответственно 20; 16; 20; 15; 24 минуты. Расчет имеет следующую схему: совокупный рабочий час врача составляет
n= 8 * 5 = 40 часов (2400 минут, или 480 минут на одного врача).
Нагрузка на одного врача определяется:
Для первого - 480:20=24 больных; для второго - 480:16=30 больных; и т.д. Суммарно - 130 больных.
Формула для расчета простого среднего гармонического имеет вид:
Хгпрм= 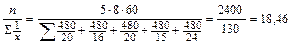 мин
мин
Среднее геометрическое определяется для тех параметров, изменения значений которых проходят в геометрической прогрессии (изменения численности населения в период между переписью, результат титрувания вакцин, прирост массы тела новорожденного на протяжении отдельных месяце жизни и др.).
Формула для расчета простой средней геометрической имеет вид:
Хгfhм= 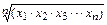
Lg Хгfhм= 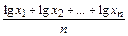
Логарифм среднего геометрического равен сумме логарифмов всех членов ряда, поделенных на их число.
Среднее арифметическое, которое используется самостоятельно, само по себе, часто имеет граничное значение потому, что оно не отображает размеры колебаний количественных вариантов ряда ( вариабельность ряда). Важной характеристикой ряда является оценка разнообразия (непостоянства, вариабельности) вариантов исследований совокупности. Основою данной оценки является определение отклонений отдельных вариантов от среднего значения ряда. Если вариационный ряд более компактный, варианты меньше отличаются от среднего арифметического. Поэтому можно считать, что данная средняя величина является более типичной и лучше описывает данную совокупность. Если вариационный ряд разбросанный, варианты значительно отличаются от среднего. В таком случае среднее является менее типичным и не совсем четко характеризует ряд и свойства отдельных его вариантов.
Одним из критериев характеристики вариантов ряда является его амплитуда - разница крайних значений. Однако, она не учитывает характер их распределения. В условиях высокой компактности распределения вариантов в совокупности и при наличии отдельных вариантов, которые резко отличаются от других, амплитуда не отображает истинный характер распределения.
Другой величиной разнообразия признаков исследований совокупности является среднее квадратическое отклонение (стандартное отклонение), которое обозначается символом "сигма" (σ). Чем выше среднее квадратическое отклонение, тем выше будет степень разнообразия признаков совокупности и меньше типичной среднее. Например, анализ организации госпитализации больных показал, что средняя продолжительность до операционного периода при плановой госпитализации в двух стационарах составляет:
Больница №1 Больница №2
X=3,1 дня X= 3,2 дня
σ=0,3 дня σ =0,9 дня.
Средняя продолжительность подготовки к операции в двух стационарах практически одинакова, однако среднее квадратичное отклонение, что отображает его колебания, в больнице №1 значительно меньше. Это свидетельствует о большой типичности средней величины и в результате о лучшей организации больничной подготовки к оперативному лечению.
В случаях, когда значения признаков больше отличаются от среднего (больница №2), обобщающая вариация находится под влиянием более разнородных условий и исследуемая совокупность больных по качеству организации их госпитализации является менее однородной. Таким образом, средняя величина , характеризующая эту менее однородную совокупность, будет менее типовой.
Формула расчета среднего квадратичного отклонения такова:
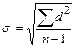 - для простого вариационного ряда;
- для простого вариационного ряда;
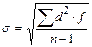 - для сгруппированного вариационного ряда.
- для сгруппированного вариационного ряда.
Где:
n-1 - число наблюдений в исследуемой совокупности ( при достаточно большом числе наблюдений n>30 - в формуле вместо n-1 подставить n);
f - частота варианта;
d=x- 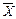 - отклонения каждого варианта от среднего арифметического;
- отклонения каждого варианта от среднего арифметического;
x - значение варианта
Для автоматизации расчетов и их программирования более удобна формула, которую можно привести в следующем виде:

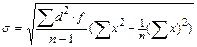 - для простого вариационного ряда;
- для простого вариационного ряда;
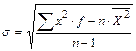 - для сгруппированного вариационного ряда.
- для сгруппированного вариационного ряда.
Методику расчета среднего квадратического отклонения рассмотрим на примере оценки средне продолжительности лечения больных с пневмонией в стационаре (табл. 2).
Таблица 2.
Дата добавления: 2015-08-04; просмотров: 756;
