Соотношение между теплотой, работой и внутренней энергией.

Для оценки доли теплоты, затраченной на изменение внутренней энергии, в термодинамике при исследовании циклов вводят коэффициент α , которым обозначают отношение

α = . (2.54)

Долю тепла, расходуемую на совершение работы расширения, обозначают через 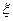, тогда

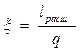или . (2.55)

Выразив изменение внутренней энергии и теплоту через теплоемкости, получим:

α = 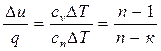и .

Таким образом, распределение теплоты между внутренней энергией и работой в процессе можно оценить по известному показателю политропы.

В теплотехнике часто используются так называемые и з о п а р а м е т- р и ч е с к и е процессы: изобарный, изохорный, изотермический и адиабатный.

2.3.3. Изобарный процесс

Процесс, протекающий при постоянном давлении, называют и з о-

б а р н ы м.

Уравнение процесса записывается в виде p = const или c_n = c_p.

Из уравнения политропы следует, что для изобарного процесса n = 0.

Соотношение параметров в начальном и конечном состояниях процесса устанавливается с использованием уравнений состояния, записанных для этих точек: p₁v₁ = RT₁ и p₂v₂ = RT₂. Поделив одно уравнение на другое, получим:

.

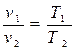В изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам.

График процесса называется и з о б а р о й. В pv–координатах (рис.2.8) изобара – прямая линия, параллельная оси удельных объемов. В координатах Ts изобара – логарифмическая кривая (рис.2.9), так как она описывается уравнением, полученным из (2.51) при n = 0:

s_i = s₁ + c_p ln . (2.56)

Крутизна изобары в Ts-координатах для каждой температуры определяется тангенсом угла наклона кривой к оси абсцисс, т.е.

tg β = ..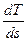

Принимая во внимание, что для изобарного процесса справедливы уравнения dq = T ds и dq = c_p dT, получим:

tg β = 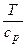. (2.57)

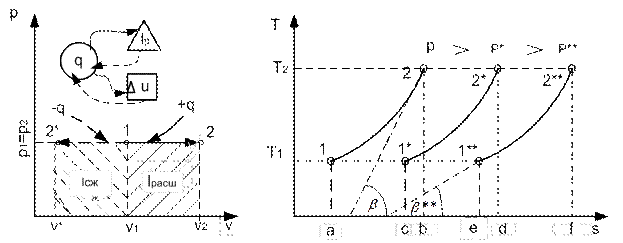
Рис. 2.8 Рис. 2.9

Отсюда следует, что с увеличением температуры и уменьшением теплоемкости крутизна изобары растет. Подкасательная к изобаре в любой точке определяет значение истинной теплоемкости c_p при температуре T .

Все изобары являются эквидистантными кривыми (на рис.2.9 изобары при р, р* и р**), так как при одной и той же температуре они имеют одинаковые угловые коэффициенты. Кроме того, расстояние между двумя изобарами вдоль оси абсцисс при разных температурах одинаково. Так при температуре T₁ отрезок ce между изобарами р^* и р^** определяется выражением:

.

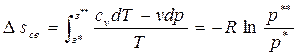Аналогично найдем отрезок d f межу теми же изобарами при температуре Т₂.

.

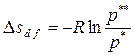В итоге получили 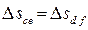или c e = d f.

Изменение внутренней энергии запишем через теплоемкость при постоянном давлении, используя для этой цели уравнение Майера:

∆u = (c_p – R) (T₂ – T₁).

Изменение энтальпии в процессе вычисляется как

∆i = c_p(T₂ - T₁).

Приращение энтропии можно записать и через c_p, и через c_v:

s₂ – s₁= c_p ln (T₂/T₁) и s₂ – s₁ = c_v ln (T₂/T₁) + R ln (v₂ /v₁).

Работа расширения выражается следующим образом:

l_расш = .

При изменении температуры на один градус работа расширения численно равна величине газовой постоянной.

Техническая работа будет равна нулю, так как dp = 0:

l_тех = - .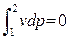

Количество теплоты, сообщаемое газу в изобарном процессе, вычисляется по уравнению:

q = c_p (Т₂ – Т₁) = i₂ – i₁.

Часть сообщенной теплоты идет на изменение внутренней энергии, а другая часть – на работу расширения.

α = , .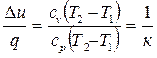

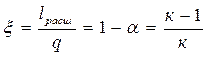2.3.4. Изохорный процесс

Процесс, протекающий при постоянном объеме, называется

и з о х о р н ы м.

Уравнение процесса записывается в виде v = const или c_n = c_v.

Показатель политропы для изохорного процесса получим из уравнения политропы, если раскроем его относительно удельного объема:

v = .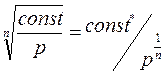

Из этого следует, что удельный объем может быть постоянным только при показателе политропы, равном n= ±∞.

Из уравнения состояния при v=const получим связь между параметрами в конечных точках процесса:

.

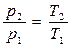Это значит, что при постоянном объеме давление газа изменяется прямо пропорционально изменению абсолютной температуры.

График процесса называется и з о х о р о й. В pv–координатах (рис.2.10) изохора – прямая линия, параллельная оси давлений. В координатах Ts изохора (рис.2.11) – логарифмическая кривая, так как текущие значения энтропии и температуры связаны уравнением:

s_i - s₁ = . (2.58)

Как и в изобарном процессе, крутизна изохоры в Ts-координатах определяется угловым коэффициентом

tg γ = T/c_v .

Из последнего выражения следует, что крутизна изохоры растет с увеличением температуры и уменьшением теплоемкости. Сравнение угловых коэффициентов изохоры и изобары показывает, что при одной и той же температуре изохора проходит круче, так как c_p>c_v.

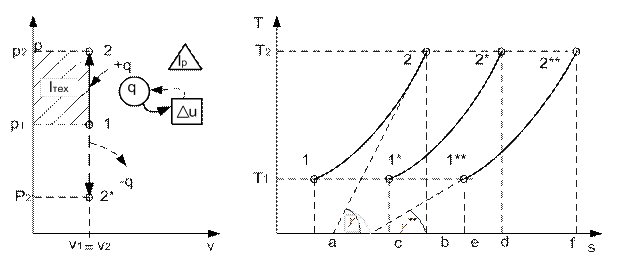
Рис. 2.10 Рис. 2.11

Изохоры, так же как и изобары, эквидистанты (рис.2.11). Как и в изобарном процессе, можно показать, что ac = bd.

Для вычисления изменения внутренней энергии, энтальпии и энтропии в процессе от начального до конечного состояний используются уравнения:

∆u = c_v(Т₂ – Т₁), ∆i = c_p(Т₂ –Т₁) и .

Работа расширения в изохорном процессе равна нулю.

Техническая работа определится по формуле:

l_тех= - .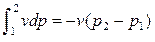

Так как l_расш = 0, то из первого закона термодинамики следует, что все подведенное тепло расходуется на изменение внутренней энергии:

q = u₂ – u₁= c_v (T₂ – T₁).

Значения α и ξ для изохорного процесса будут равны:

α = 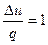и ξ =1 – α = 0.

2.3.5. Изотермический процесс

Процесс, протекающий при постоянной температуре, называется и з о т е р м и ч е с к и м.

Уравнение процесса записывается в виде Т = const или

pv = const. (2.59)

Следовательно, показатель процесса n = 1, а теплоемкость с_T = ± .

Отсюда же: отношение удельных объемов обратно пропорционально отношению давлений, т.е.

.

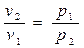График процесса, построенный по уравнению (2.59), называют и з о-

т е р м о й. В pv– координатах (рис.2.12) изотерма – равнобочная гипербола.

В координатах Ts изотерма – прямая линия параллельная оси абсцисс, рис.2.13..

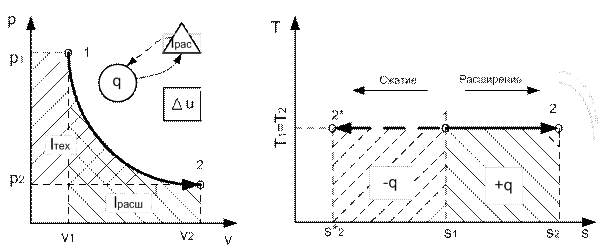
Рис. 2.12 Рис. 2.13

Изменения внутренней энергии и энтальпии в процессе равны нулю, т.е. du = c_vdT = 0 и di =c_pdT = 0.

Изменения энтропии в изотермическом процессе можно выразить через удельный объем и через давление:.

ds = .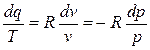

Интегрируя данное выражение от первого состояния до второго, получим :

∆ѕ=ѕ₂ –ѕ₁=R ln . .

Для изотермического процесса работа расширения равна технической работе:

l_расш = 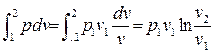= RT₁ln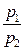

и l_тех = -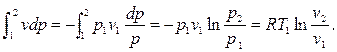

Теплота, участвующая в процессе

q = T (s₂ – s₁) =RT ln 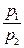= RT ln .

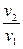В данном процессе все тепло, подведенное к газу, идет на совершение работы расширения:

Коэффициент α для изотермического процесса равен нулю, значение ξ - единице, т.е.

α = 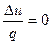и ξ = 1 – α = 1.

2.3.6. Адиабатный процесс

А д и а б а т н ы м называют процесс изменения состояния системы, происходящий без теплообмена с окружающей средой.

В адиабатном процессе dq = 0, следовательно, теплоемкость с_q = 0.

Для вывода уравнения адиабаты используем выражения первого закона термодинамики (1.17) и (1.18) при dq = 0:

c_p dT –v dp = 0 и c_v dT + p dv = 0

Разделим первое уравнение на второе:

,

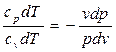сократив на dT, разделив переменные и обозначив c_p/c_v =к, будем иметь:

к

Проинтегрировав полученное уравнение от начального до конечного состояния процесса, получим:

к ln

или

p₁ v₁^к = p₂ v₂^к.

На основании этого запишем уравнение адиабаты:

p v^к = const. (2.60)

При адиабатном процессе произведение давления на удельный объем в степени к есть величина постоянная. Кривую, построенную по уравнению (2.60), называют а д и а б а т о й, а величину к, являющуюся отношением теплоемкостей c_p и c_v – п о к а з а т е л е м а д и а б а т ы.

Уравнение адиабатного процесса аналогично политропному, разница лишь в том, что здесь вместо показателя политропы п имеем показатель адиабаты к. Поэтому все последующие соотношения для адиабатного процесса получим из политропных, заменив п на к.

Так, связь между параметрами в адиабатном процессе имеет вид:

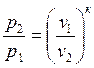или ;

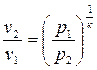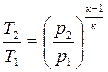
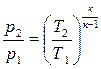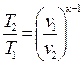или ;

или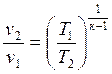

Адиабата в pv-координатах представляет собой неравнобочную гиперболу, рис.2.14. Она круче изотермы, так как к >1. В Ts-координатах адиабата изображается вертикальной прямой, рис. 2.15, потому что при q = 0 изменения энтропии нет, т.е. ∆s = 0. В этом случае адиабатный процесс можно называть и з о э н р о п н ы м процессом

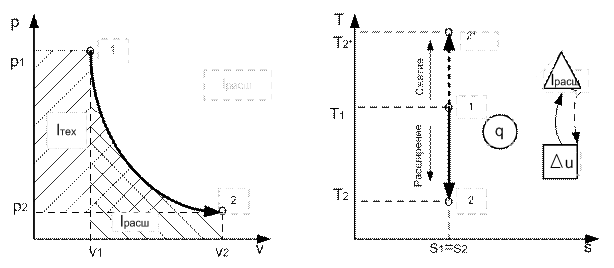
Рис. 2.14 Рис. 2.15

Изменение энтальпии и внутренней энергии определяются по уравнениям:

∆i =c_p (T₂ –T₁) и ∆u = c_v (T₂ – T₁) .

Заменив в уравнении (2.52) и (2.53) п на к, получим работу расширения и техническую работу:

l_расш =и l_тех = ..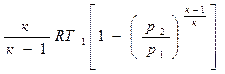

Отсюда следует, что в адиабатном процессе техническая работа в к раз больше величины работы расширения.

Поскольку теплота в адиабатном процессе равна нулю, то работа расширения совершается только за счет изменения внутренней энергии рабочего тела.

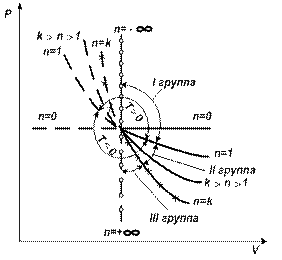
2.3.7. Характерные группы политропных процессов

В зависимости от энергообмена системы с окружающей средой поли- тропные процессы расширения можно разбить на три характерные группы:

I группа – с показателем процесса п от -∞ до 1;

II группа – с показателем процесса п от 1 до к;

III группа – с показателем процесса п от к до +∞.

Распределение процессов по группам в pv и Ts – координатах показано на рис.2.16.(а) и рис.2.16 (б), соответственно. Процессы, лежащие выше изотермы, протекают с увеличением внутренней энергии, ниже – с ее уменьшением. К процессам, расположенным над адиабатой, теплота подводится, под адиабатой – отводится. Процессы расширения лежат справа от изохоры, сжатия – слева.

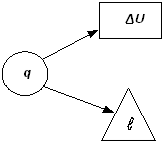
Для первой группы характерным является то, что все процессы расширения идут с подводом тепла и увеличением внутренней энергии. Связь между теплотой, работой и внутренней энергией можно представить схематически, рис.2.17. В первой группе процессов (а) вся теплота идет на совершение

работы расширения и увеличение внутренней энергии.

а) б)

Рис.2.16

а) б) в)

Рис. 2.17

Во второй группе (б) теплота тоже подводится, но внутренняя энергия уменьшается. В этом случае работа расширения совершается за счет подведенного тепла и уменьшения внутренней энергии.

Третью группу (в) отличает то, что все процессы расширения идут с отводом теплоты и уменьшением внутренней энергии. Работа процессов этой группы производится только за счет уменьшения внутренней энергии. Кроме того, внутренняя энергия дополнительно еще уменьшается вследствие отвода теплоты от системы.

2.3.8. Диаграммы состояния

Изображение процессов в координатах, по осям которых выбраны те или иные параметры. позволяет построить для рабочих тел характерные диаграммы состояния, широко использующиеся при исследовании термодинамических процессов и циклов. Рассмотрим некоторые из них.

Диаграмма состояния в pv – координатах представляет собой сетку из изобар и изохор, на которую наложены изотермы. По этой диаграмме можно быстро определить в любом состоянии термодинамические параметры рабочего тела, для которого она построена. Однако pv-диаграмма дает недостаточно полную информацию о рабочем теле и процессах изменения его состояния.

Диаграмма состояния в Ts – координатах позволяет непосредственно определить большее число параметров, так как на поле графика, состоящего из сетки изотерм и изоэнтроп, наносятся уже два вида изопараметрических процессов: изохоры и изобары. По этой диаграмме для любого состояния можно определить T, p, v, s, а также c_p и c_v.

Некоторым недостатком рассмотренных диаграмм является то, что при определении количества работы (в pv – диаграмме) и количества теплоты

(в Ts – диаграмме) приходится измерять соответствующие площади.

В технических расчетах чаще используется диаграмма, построенная в is-координатах. Достоинством такой диаграммы является то, что на ней работа и теплота процессов изображаются отрезками линий. При построении диаграммы по оси ординат откладывается энтальпия, а по оси абсцисс – энтропия. На рис. 2.18 представлена is – диаграмма водяного пара. На поле графика из изоэнтальп и изоэнтроп наносятся изобары, изохоры и изотермы.

Имея is – диаграмму, по двум известным параметрам можно просто найти остальные параметры состояния рабочего тела. Так, например, по p и T непосредственно определяются i , s, v, c_p, c_v и вычисляются R, к, u. В адиабатном процессе расширения от состояния 1 до состояния 2 отрезок оси ординат i₁ - i₂ представляет работу техническую, а в изотермном процессе 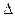s = s₂ – s₁ – эквивалентна теплоте, подведенной в процессе расширения.

В холодильной технике, как правило, используются диаграммы состояния хладагентов в координатах ln p – i. Для фреона R–22 диаграмма состояния представлена в Приложении табл. 16.

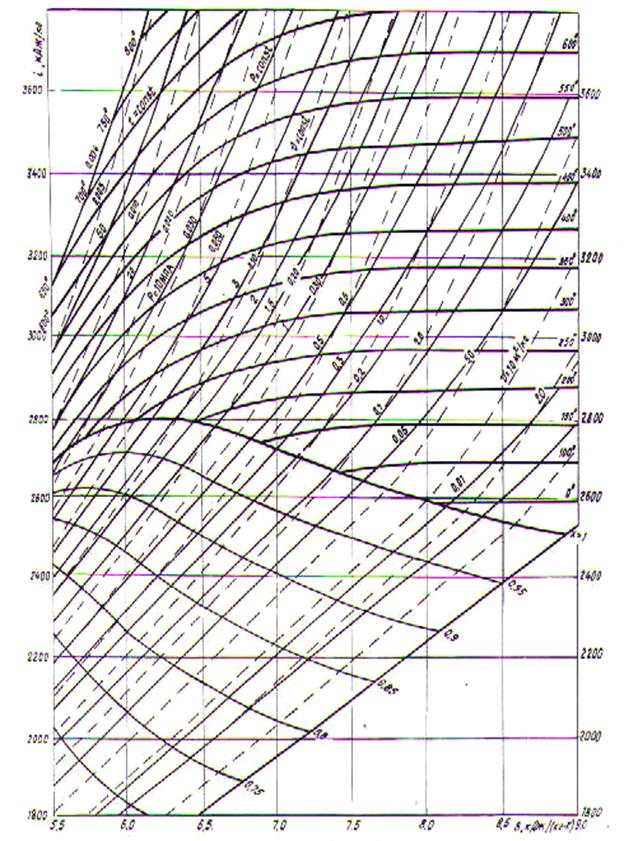
Рис. 2.18