Оптимизация контура положения для режима средних перемещений

Наилучшим считается такой процесс отработки средних перемещений, при которой скорость двигателя изменяется по треугольному графику (это позволяет максимально использовать перегрузочную способность двигателя, т.к. он работает только в пусковых и тормозных режимах). Чтобы обеспечить такой процесс отработки, коэффициент регулятора положения должен быть своим для каждого задающего сигнала, т.е. К_рп = f(q₃).

Принимаем упрощающее допущение: Т_т = 0 – эквивалентная постоянная времени контура тока, отсюда

1) 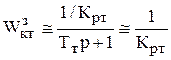– контур тока стал безинерционным;

2) 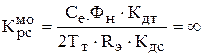– т.е. при таком регуляторе малейший сигнал на входе регулятора будет вызывать ограничение, т.е. задание будет на максимальный ток, который тут же будет отработан.

Диаграмма сигналов при отработке средних перемещений представлена на рисунке 6.11.

Будем полагать, что система статическая, но несмотря на то, что d^*_C 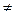0 полагаем, что она очень мала и стремится к нулю.

В момент t₀ скачком подается сигнал задания 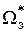и если он велик, то регулятор положения выходит на ограничение. Сразу же выйдет на ограничение и регулятор скорости, т.к. К_рс , что определяет максимальный сигнал задания на ток, который будет мгновенно отработан, т.к. контур тока является безинерционным. Начинается разгон с постоянным ускорением. В момент времени t₁ регулятор положения (РП) сойдет с ограничения и в дальнейшем его выходной сигнал будет изменяться по закону U_рп^* = . 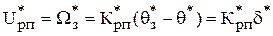Двигатель продолжает разгон с тем же d^* ускорением (т.к. заданная скорость больше фактической и РС находится на ограничении того же знака). В момент t₂ заданная скорость будет равна фактической .

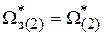В следующие моменты фактическая скорость будет превышать заданную величину, поэтому РС выходит на ограничение этого другого знака, что мгновенно отрабатывается контуром тока. Двигатель переходит в тормозной режим с постоянным ускорением. Процесс заканчивается в точке t₃, когда фактическое перемещение станет равным заданному (при условии d_С = 0).

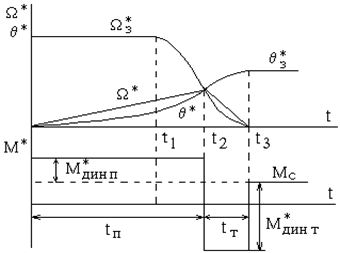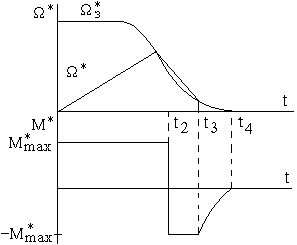Рисунок 6.11 Рисунок 6.12

Целью последующего расчета будет нахождение К_рп = f(q₃) – коэффициента регулятора в функции задающего сигнала.

t_P = ? M_м- M_c = J = = ;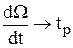

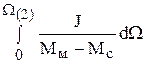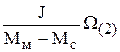t_T = ? –M_M – M_C = J = – = ;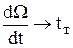

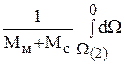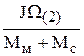t_P + t_T =? t_P + t_T = JW₂ = =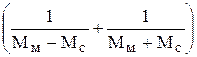

= .

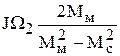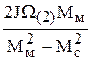Найдем величину перемещения при отработке за весь цикл

q = q₃ = = = = =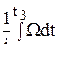

= = .

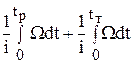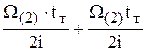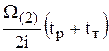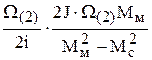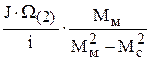Перейдем к относительным единицам

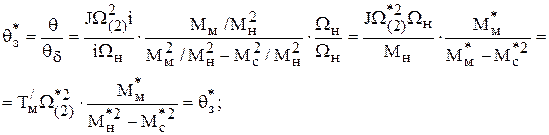
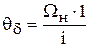= Т^/_М.

JW_H/М_н = Т^/_М – время разгона до W_H с M_н.

,

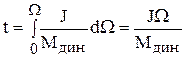где М_дин = J .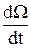

t_P/W = W_H = 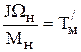– время разгона привода до номинальной скорости с номинальным моментом.

Т^/_м »1сек; Т_м = r_а×Т^/_ам.

.

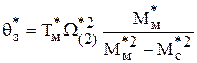В момент времени t₂ W*_С3(2) = К*_РП (q^/₃ -q^*₍₂₎) = W^*₍₂₎.

Подставим значение W^*₍₂₎ в выражение величины перемещения при отработке за весь цикл в относительных единицах

q^*₃ = Т^/_м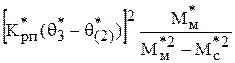

Отсюда, коэффициент регулятора положения

.

.

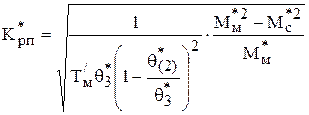Чтобы обеспечить отработку q₃ без перерегулирования и дотягивания, т.е. оптимально, коэффициент регулятора К_РП должен быть разным для разных q₃. При других сигналах задания q₃ и неизменном коэффициенте регулятора графика и скорости будут отличаться от треугольного.

Диаграмма сигналов при отработке нового перемещения q₃^*/<q₃^* представлена на рисунке 6.12.

.

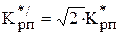До точки t₂ процесс идет точно так же, как и в предыдущем случае. Сам же момент t₂ наступит раньше.

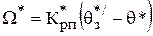= W^*₍₂₎.

В момент времени t₃ сигналы заданной и фактической скорости вновь будут равны, и регулятор скорости сойдет с ограничения. При большом К_рп примерное равенство W₃ и W_ФАКТ будет соблюдаться на протяжении всего оставленного пути. Момент двигателя при этом снижается и позиционная система доходит до точки t₄ с дотягиванием (будет пульсирующий режим).

В случае 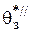> 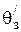, перемещение будет отрабатываться с перерегулированием.

С дотягиванием система предпочтительнее, поэтому расчет П-регулятора положения ведут для так называемого настроечного перемещения, которое является максимальным при отработке по треугольной тахограмме (рисунок 6.13).

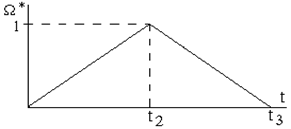Рисунок 6.13

.

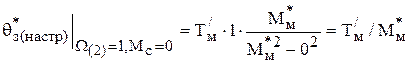Отсюда, настроечный коэффициент регулятора положения равен

К_рп^*= .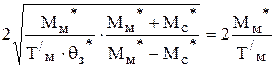

При таком коэффициенте регулятора настроечное перемещение будет отработано оптимально, а все перемещения меньше настроечного будут отрабатываться с дотягиванием.