Оптимизация контура положения для режима малых перемещений
Полагаем, что контура тока и скорости уже оптимизированы и остается оптимизировать только контур положения. Тогда структурная схема примет вид, представленный на рисунке 6.4.
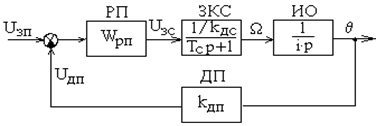Рисунок 6.4
|
Передаточная функция замкнутого контура скорости, оптимизированного на модульный оптимум имеет вид
,
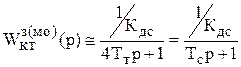где Тс = 4Тт – малая постоянная времени оптимизированного контура скорости (Тсмо = 2Тт, ТсСО = 4Тт).
Настроим контур на модульный оптимум. При такой настройке ЛАЧХ имеет вид, представленный на рисунке 6.5.
Тогда передаточная функция разомкнутого контура положения, настроенного на модульный оптимум, примет вид
,
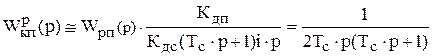где Кдп, Кдс – коэффициент передачи датчика положения и скорости соответственно.
Передаточная функция регулятора положения будет равна
,
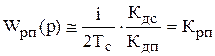где i – передаточное число редуктора.
.
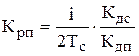Получили П-регулятор положения и астатическую систему по заданию.
,
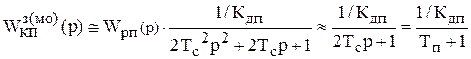где Тп = 2Тс – эквивалентная постоянная времени оптимизированного на модульный оптимум контура положения.
Тп = 2Тс = ... = 8Тm
Полученная система по заданию является астатической 1-го порядка по заданию. Если контур скорости был оптимизирован на СО и регулятор скорости был ПИ, то данный контур положения будет астатическим даже с П-регулятором.
Знак ошибки зависит от направления действия статического активного момента (см. рисунок 6.6).
 
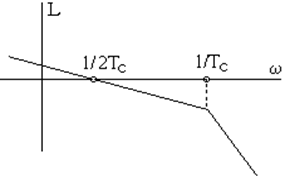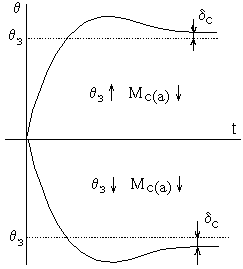Рисунок 6.5 Рисунок 6.6
|
Оценим точность позиционной системы (см. рисунок 6.7).
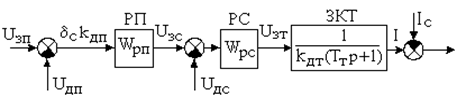Рисунок 6.7
|
; 
;
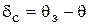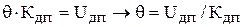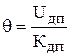– фактическое значение перемещения.
По аналогии находим заданное перемещение
.
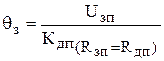Считаем, что коэффициент регулятора по заданию и каналу ОС одинаковы, т.е. Rзп = Rдп.
Определим величину ошибки
;
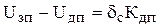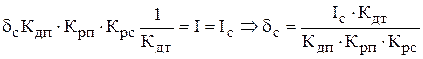– не зависит от величины задающего сигнала, а зависит от момента на валу и параметров системы.
Если контур скорости настроен на СО (регулятор скорости ПИ), то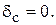 
Дата добавления: 2015-08-04; просмотров: 765;