Оптимизация контура на СО, объект которого содержит интегрирующее звено и звено с малой постоянной времени
Применим ПИ-регулятор с передаточной функцией
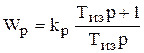 .
.
С ПИ-регулятором астатическим по заданию и возмущению передаточные функции разомкнутого и замкнутого контуров:
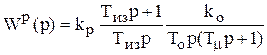 ;
;
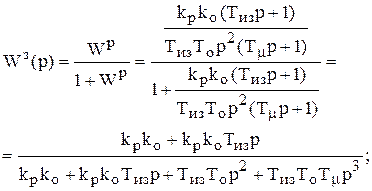
2а0а2 = а12 ® 2kpk0ТизТ0 = kp2k02Тиз2 ® 2Т0 = kpk0Тиз;
2а1а3 = а22 ® 2kpk0Тиз2Т0Тm = Тиз2Т02 ® 2kpk0Tm = T0;
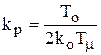 ;
; 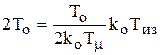 ; Тиз = 4Тm;
; Тиз = 4Тm;
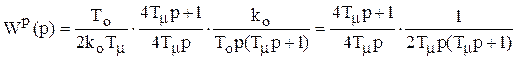 .
.
В соответствии с рисунком 5.12, ЛАЧХ разомкнутого контура получилась симметрично относительно частоты среза. Это настройка на симметричный оптимум.
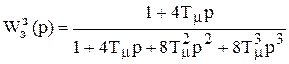 .
.
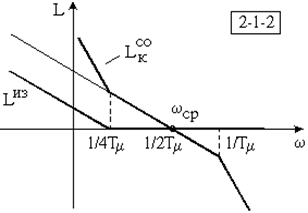 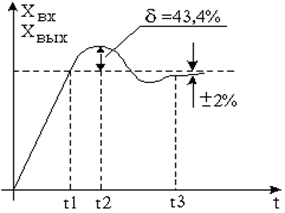 Рисунок 5.12 Рисунок 5.13
Рисунок 5.12 Рисунок 5.13
|
Передаточная функция замкнутого контура определяется только Тm. Этой передаточной функции соответствует переходный процесс, представленный на рисунке 5.13.
t1 = 3,1Tm; t3 = 16,5Tm; d = 43,4%.
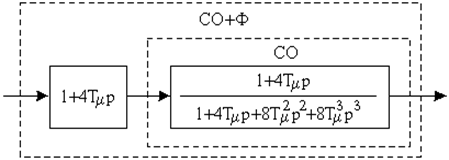 Рисунок 5.14
Рисунок 5.14
|
Повышенное перерегулирование вызвано наличием форсирующего члена в числителе передаточной функции. Такое перерегулирование недопустимо. Для снижения перерегулирования на входе замкнутого контура включают фильтр (см. рисунок 5.14).
Передаточная функция фильтра
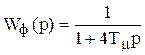 ;
;
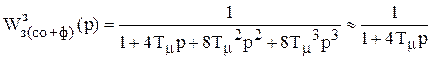 .
.
График переходных процессов при различных настройках контура представлен на рисунке 5.15.
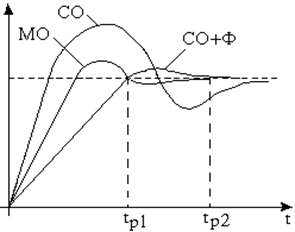 Рисунок 5.15
Рисунок 5.15
|
Таблица 5.1. Характеристики переходных процессов при различных настройках контура
| СО | МО | СО+Ф | |
| s , % | 43,4 | 4,3 | 8,1 |
| t1 | 3,1Тm | 4,3Тm | 7,6Тm |
| t3 | 16,6Тm | 8,4Тm | 13,3Тm |
Сравнивая настройку на СО и МО можно сделать вывод, что настройка на МО имеет малое перерегулирование и большое быстродействие, но при этом система является статической. Быстродействие и перерегулирование при оптимизации на симметричный оптимум (СО) вдвое хуже, чем при настройке на МО, но система становится астатической.
Перерегулирование с фильтром на входе снижается по причине замены скачка сигнала с выхода фильтра, т.е. на входе контура экспонентой.
Техническая реализация фильтра на входе системы представлена на рисунке 5.16.
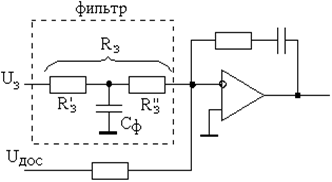 Рисунок 5.16
Рисунок 5.16
|
Применение ПИ-регулятора для объекта, содержащего интегрирующее звено и звено с малой постоянной времени позволяет построить систему астатическую по заданию и возмущению.
Дата добавления: 2015-08-04; просмотров: 709;
