Закон полного тока
Наряду с законом Био-Савара-Лапласа, для расчета магнитных полей используется закон полного тока (теорема о циркуляции).
Циркуляцией вектора 
(или 
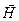) по произвольному замкнутому контуру 
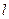называется интеграл
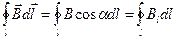,(13.6)
где 
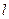- элемент контура , направленный вдоль его обхода, 
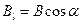- проекция вектора на направление касательной к контуру , 
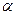- угол между векторами и .
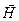Закон полного тока гласит следующее: циркуляция вектора (или ) по произвольному замкнутому контуру 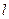прямо пропорциональна алгебраической сумме токов, охватываемых этим контуром:
, 
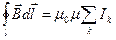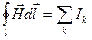,(13.7)
где суммирование ведется по всем проводникам с токами внутри контура 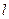. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Рассмотрим несколько примеров расчета магнитных полей.
1. Магнитное поле в центре круглого витка радиусом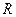 
с током 
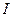(рис. 13.4).
|
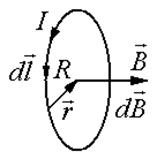
| Рис. 13.4 |
Для расчета воспользуемсязаконом Био-Савара-Лапласа. В силу симметрии все элементы витка создают в центре магнитное поле одинакового направления - вдоль нормали. Поэтому сложение векторов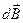 
можно заменить сложением их модулей. Поскольку все элементы проводника перпендикулярны радиусу-вектору 
( 
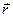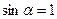) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (13.5),
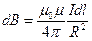, или
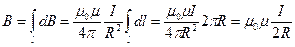. (13.8)
2. Магнитное поле прямого тока 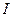, т.е. тока, текущего по тонкому прямому бесконечному проводу. Картина магнитного поля показана на рис. 13.5. Выберем замкнутый контур в виде окружности радиуса 
. В каждой точке этого контура вектор одинаков по модулю и направлен по касательной к окружности, при этом векторы и коллинеарны (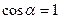 
).
|
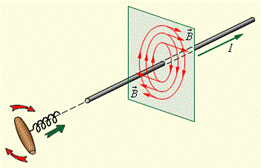
| Рис. 13.5 |
Следовательно, циркуляция вектора (13.7)
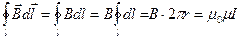, или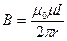 
.(13.9)
Таким образом, исходя из теоремы о циркуляции вектора , мы получили выражение для магнитной индукции поля прямого тока.
Сравним циркуляции векторов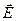 
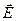и . Циркуляция вектора электростатического поля всегда равна нулю, т. к. электростатическое поле является потенциальным полем. Циркуляция вектора магнитного поля никогда не равна нулю. Такое поле называется вихревым.
Дата добавления: 2015-08-04; просмотров: 1775;