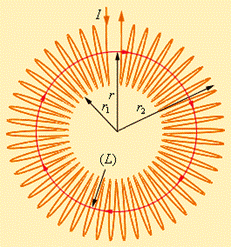
Магнитное поле тороида (тороидальной катушки).

Предположим, что катушка с током 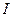, содержащая 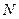витков, плотно намотана на магнитный тороидальный сердечник с относительной магнитной проницаемостью 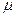. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности (рис. 13.6).

Применим закон полного тока к контуру 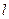в виде окружности радиуса , проведенной по средней линии тороида. Из соображения симметрии ясно, что модуль вектора одинаков вдоль всей этой линии. По теореме о циркуляции (13.7) получим:

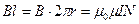, или 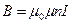, (13.10)

где 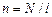- число витков на единицу длины тороида.

Отметим, что формула (13.10) справедлива и для длинного соленоида (длинной прямолинейной катушки).

Рис. 13.6

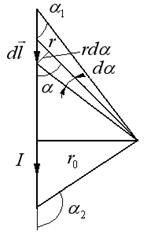
4. Магнитное поле прямого проводника с током 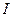конечной длины(рис. 13.7).

Рис. 13.7

Для расчета воспользуемсязаконом Био-Савара-Лапласа. Модуль вектора магнитной индукции в точке А поля от элемента прямого проводника с током 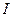равен

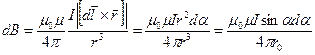,(13.11)

где 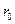- кратчайшее расстояние от точки А до оси провода, .

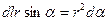Векторы 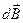всех малых элементов провода в точке А направлены одинаково – на нас перпендикулярно плоскости чертежа. Модуль суммарного магнитного поля равен сумме модулей векторов 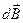, т.е.:

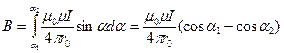, (13.12)

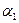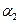где и - углы между вектором (совпадает с направлением тока 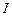) и радиус-векторами, проведенными из концов провода к точке наблюдения А.

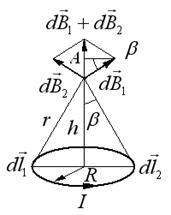
5. Магнитное поле кругового витка с током 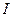(рис. 13.8).

Рис. 13.8

Рассчитаем магнитное поле в точке наблюдения А на оси кругового тока 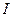радиуса 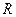на расстоянии 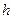от плоскости витка, используя закон Био-Савара-Лапласа:

.

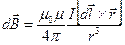Векторы и 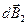для полей двух диаметрально противоположных элементов витка 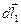и 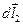, имеющих одинаковую длину ( 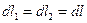), равны по модулю:

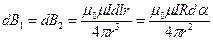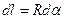, . (13.13)

Результирующий вектор 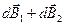в точке наблюдения А направлен по оси витка, причем

, ,

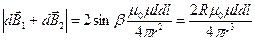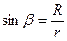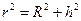. (13.14)

Интегрируя последнее соотношение по половине дуги окружности 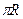, получим окончательно:

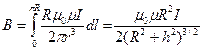. (13.15)

Отметим, что круглый виток с током называется магнитным диполем. Его магнитное поле (13.15) подобно (дуально) напряженности электростатического поля электрического диполя на его оси [2]:

.

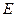
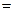
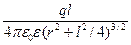6. Магнитное поле соленоида.

Соленоидом называется длинная катушка, состоящая из большого числа витков. На рис. 13.9 изображено магнитное поле соленоида конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно (постоянно) и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.

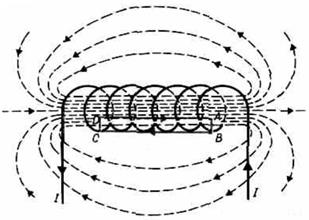
Рис. 13.9

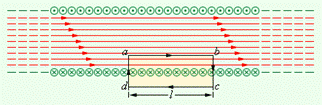
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции 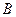можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 13.10.

Рис. 13.10

Вектор магнитной индукции 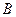отличен от нуля только вдоль стороны ab замкнутого контура abcd. Следовательно, используя закон полного тока (13.7), получим:

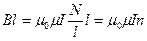, (13.16)

где 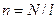- число витков соленоида на единицу длины. Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки (13.10).

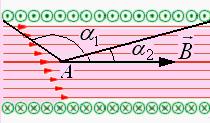
Магнитная индукция поля внутри соленоида конечной длины на его оси в точке наблюдения А (рис. 13.11) [2]:

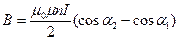, (13.17)

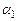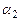где и - углы между вектором 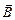на оси соленоида и радиус-векторами, проведенными из точки наблюдения А на оси к концам соленоида.

Рис. 13.11