Сила Лоренца. Ускорители заряженных частиц

Сила Ампера, действующая на отрезок проводника с током 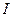длиной 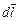, находящийся в магнитном поле (13.18), может быть выражена через силы, действующие на отдельные носители заряда.

Найдем силу Лоренца 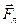, действующую на элементарный носитель заряда 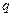при его движении в однородном магнитном поле с индукцией .

Пусть концентрация носителей свободных зарядов в проводнике с током равна 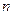. Поскольку ток равен отношению количества заряда 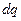, прошедшего через площадку 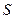за время 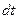, к величине этого промежутка времени 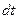, то

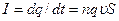, (13.20)

где 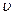– модуль скорости 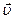упорядоченного движения носителей заряда по проводнику, 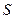– площадь поперечного сечения проводника.

Подставив (13.20) в (13.18), и поделив силу Ампера на число 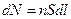носителей заряда в проводнике длиной , сечением 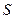, получим:

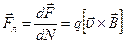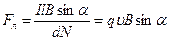, ,(13.21)

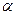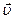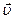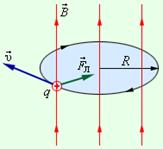
где - угол между векторами и . Векторы , и 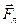образуют правую тройку векторов (рис. 13.14).

Рис. 13.14

Из формулы (13.21) видно, что сила Лоренца 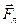всегда направлена перпендикулярно скорости частицы 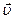. Она может изменить только направление вектора скорости частицы 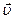, но не его величину. Работа силы Лоренца по перемещению заряда 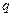всегда равна нулю, поскольку .

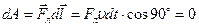Для положительных зарядов направление силы Лоренца определяется по правилу левой руки: за на­правление тока нужно брать на­правление вектора скорости поло­жительного заряда. Для случая движения отрицательно заряженных частиц (например, электронов) четыре паль­ца следует располагать противо­положно направлению вектора скорости или использовать правую руку.

Отметим, что магнитное поле, в отличие от электрического поля, не действует на покоящиеся заряды ( ).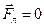

Сила Лоренца равна нулю и в случае, когда вектор скорости частицы 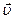и вектор магнитной индукции коллинеарны, т.е. направлены в одну сторону. При этом частица будет двигаться равномерно и прямолинейно.

Если вектор скорости 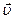частицы в однородном магнитном поле направлен перпендикулярно вектору магнитной индукции (рис. 13.14), то частица будет двигаться равномерно по окружности радиуса 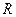, что следует из второго закона Ньютона:

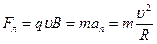, . (13.22)

При этом время одного оборота (период обращения) не зависит от скорости:

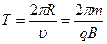. (13.23)

Рассмотрим случай, когда поле направлено по оси 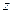, а вектор скорости 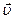частицы имеет компоненту 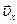по оси 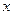и компоненту 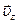по оси 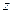, параллельную вектору . В этом случае частица движется по спирали (рис. 13.15), совершая равномерное движение вдоль силовой линии и одновременно двигаясь по окружности в перпендикулярной плоскости ( 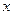, ). Радиус спирали 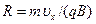, шаг спирали .

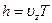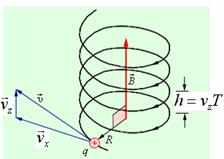
Рис. 13.15

Если частица движется одновременно в магнитном и электрическом полях, то на нее действует и сила Кулона, и сила Лоренца:

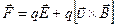. (13.24)

Характер и траектория движения частицы зависит от взаимной ориентации векторов 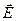, и .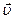

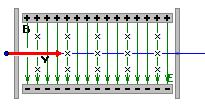
В целом ряде устройств, например, в масс-спектрометре, необходимо предварительно осуществить селекцию заряженных частиц по скоростям. Этой цели служат селекторы скорости, в которых частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, а магнитное поле создается в зазоре между полюсами электромагнита. Начальная скорость 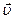заряженных частиц направлена перпендикулярно векторам 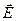и .

На частицу в скрещенных полях действует электрическая сила Кулона и магнитная сила Лоренца. Когда эти силы равны по величине и противоположны по направлению, заряженная частица будет двигаться внутри конденсатора равномерно и прямолинейно рис. 13.16.

Такая частица, пролетев конденсатор, пройдет через небольшое отверстие в перпендикулярно расположенном экране. Условие прямолинейной траектории частицы

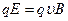. (13.25)

Рис. 13.16

Это условие не зависит от заряда и массы частицы, а зависит только от ее скорости 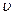. При заданных электрическом и магнитном полях селектор выделит частицы, движущиеся по скоростью

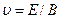. (13.26)

Остальные частицы не пройдут отверстие в экране.

После селектора скорости частицы влетают в масс-спектрометр. Это устройство позволяет измерять массы частиц c известным зарядом 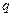, например, ионов или ядер различных атомов. Движение заряженных частиц в масс-спектрометре показано на рис. 13.17.

Рис. 13.17

Напомним, что ион – это атом, в котором нарушено равновесие между зарядом ядра (заряд ядра складывается из общего заряда протонов) и общим зарядом электронной оболочки.С последнего уровня электронной оболочки можно «забрать» один или несколько электронов и тогда атом становится положительным ионом или добавить электроны – получим отрицательный ион.

Масс-спектрометры используются также для разделения изотопов, т.е. ядер атомов с одинаковым зарядом, но разными массовыми числами, например, изотопов урана 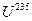₉₂ и ₉₂ .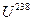

Для обозначения ядер химических элементов используются следующие символические обозначения:

,

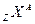где 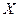- символ химического элемента, - зарядовое число, оно соответствует номеру элемента в периодической таблице Менделеева и показывает число протонов в ядре. Заряд протона положительный, он равен элементарному заряду 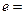1,6∙10^-19 Кл (заряд электрона отрицательный, он равен минус 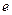). Зная число ,можно найти заряд ядра

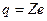. (13.27)

Атомное ядро состоит их протонов и нейтронов (их называют нуклонами). Общее число нуклонов в атомном ядре называется массовым числом 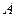. Масса покоя протона

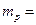1,6726·10^-27 кг 1,00728 а.е.м. 1836 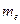, (13.28)

масса покоя нейтрона

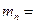1,6749·10^-27 кг 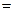1,00867 а.е.м. 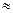1839 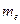, (13.29)

где 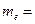9,11·10^{-31 кг – масса покоя электрона, а.е.м. – атомная единица массы:}

1 а.е.м. 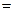1,66·10^{-27 кг.}

Поскольку 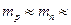1 а.е.м., то масса ядра

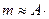1,66·10^-27 кг. (13.30)

Масс-спектрометр состоит из камеры с высоким вакуумом. Камера помещена в однородное магнитное поле в пространстве между полюсами электромагнита. Частицы влетают в камеру с большими скоростями в плоскости, перпендикулярной магнитному полю, и под действием силы Лоренца начинают движение по окружности радиуса 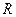(13.22).

С помощью масс-спектрометра можно разделять однократно ионизированные атомы изотопов, наприме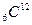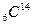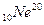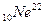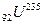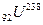р, - , - , - и др.

Заряд этих частиц одинаков и равен заряду протона 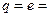1,6∙10^-19 Кл, а массы различны и определяются формулой (13.27)

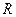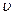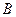Измеряя радиус при известных значениях и , определяют отношение :

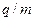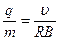. (13.31)

В случае частиц с одинаковыми зарядами 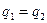и скоростями 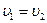масс-спектрометр позволяет разделить частицы с разными массами. Из (13.31) следует, что отношение масс двух частиц одного элемента равно отношению радиусов их траекторий и отношению их массовых чисел:

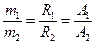. (13.32)

Кроме масс-спектрометров, в ядерной физике широко используются ускорители заряженных частиц (электронов, протонов, атомных ядер, ионов и т.д.), в которых частицы приобретают кинетическую энергию в несколько миллионов электронвольт (МэВ). Простейший ускоритель, который называется циклотроном, приведен на рис. 13.18.

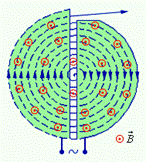
Рис. 13.18

Ускоритель состоит из двух половинок (дуантов). Магнитное поле перпендикулярно плоскости чертежа и направлено на нас. Между дуантами имеется узкая щель. Дуанты с помощью электродов подключены к электрогенератору, создающему в щели переменное электрическое поле.

Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.

Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма - периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны, т.е. частота электрогенератора совпадает с частотой вращения частиц по окружности. При этом два раза за период, когда частица пролетает щель, она ускоряется за счет энергии электрического поля. В результате частица движется по спирали, многократно ускоряясь в щелях. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.

На выходе циклотрона частица приобретает огромную кинетическую энергию. Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ.