Общее условие устойчивости
Чтобы линейная импульсная система была устойчивой достаточно чтобы модули собственных значений матрицы А были меньше единицы.
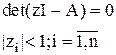
Доказательство
Будем искать частные решения разностного уравнения для объекта
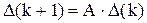
в виде 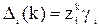 .
.
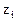 - корень характеристического уравнения
- корень характеристического уравнения
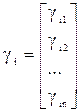 - соответствующий этому корню собственный вектор
- соответствующий этому корню собственный вектор
Общее решение тогда можно записать как линейную комбинацию частных решений:
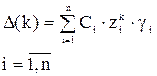
Подставим частное решение в исходное разностное уравнение:
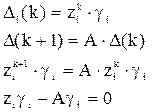
Получаем систему уравнений для нахождения неизвестного собственного вектора gi
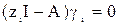 (*)
(*)
Обращаем внимание на то, что матрица в круглых скобках вырожденная, поэтому система вида (*) недоопределена, вектор gi имеет бесконечное множество значений. Для нахождения любого из них произвольно зададим одну из компонент этого вектора.
Из системы исходных уравнений исключают зависимое уравнение, остальные компоненты вектора gi находят по сформированной системе уравнений (n-1) порядка. Для нахождения неизвестных констант Сi используются начальные условия:
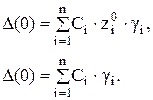
Это система из n уравнений для нахождения констант 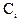 .
.
Дата добавления: 2015-08-04; просмотров: 1020;
