Гармонические колебания. В качестве примера рассмотрим колебания пружинного маятника без затухания (рис
В качестве примера рассмотрим колебания пружинного маятника без затухания (рис. 1.1). Дифференциальным уравнением движения этого идеализированного осциллятора является уравнение второго закона Ньютона.

Рис. 1.1
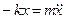 .
.
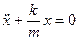 или
или 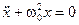 . (1.1)
. (1.1)
Общее решение уравнения (1.1) — гармоническая функция смещения от времени
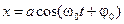 . (1.2)
. (1.2)
Скорость груза m тоже меняется по гармоническому закону
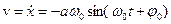 (1.3)
(1.3)
Здесь α — амплитуда,
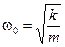 — частота собственных незатухающих колебаний,
— частота собственных незатухающих колебаний,
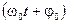 — фаза,
— фаза,
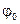 — начальная фаза колебания.
— начальная фаза колебания.
Начальные условия колебания позволяют определить его амплитуду (α) и начальную фазу ( 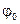 ).
).
Пусть при t = 0, координата x(0) = x0, а скорость 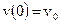 .
.
Запишем уравнения (1.2) и (1.3) для момента времени t = 0:
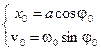
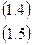
Отсюда следует, что
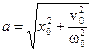 и
и 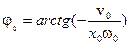 . (1.6)
. (1.6)
Дата добавления: 2015-08-04; просмотров: 690;
