Переход от оригинала к изображению.
Операторный метод расчета переходного процесса.
В операторном методе происходит алгебраизация уравнений, от функций вещественной переменной t переходим к функции комплексной переменной p = δ+jω .
Функция вещественной переменной называется оригиналом. Функция комплексной переменной – изображением (отображением). При этом операции интегрирования и дифференцирования заменяются на деление и умножение на р , что приводит к алгебраизации уравнений. После этого все методы расчета цепей синусоидального тока становятся применимыми к так называем оператором схемы, который используется в операторном методе.
Переход от оригинала к изображению.
Для перехода от функции оригинала к функции изображения применяется интеграл Лапласа (преобразования Лапласа).
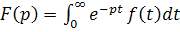 (1)
(1)
f(t) – оригинал;
F(p) – изображение;
f(t) ÷ F(p)
Интеграл Лапласа сходится, если f(t) удовлетворяет следующим условиям:
1) Условия Дирихле (разрывы и непрерывности 1-го рода)
2) f(t) задана при t > 0
3) f(t) растет не быстрее показательной функции еδt.
Все функции в электротехнике удовлетворяют этим условиям.
Дата добавления: 2015-08-04; просмотров: 767;
