Уравнение изотермы мономолекулярной адсорбции Ленгмюра.

Уравнение получено Ленгмюром для границы раздела твердое тело–газ, однако, оно может быть распространено и на границе жидкость–газ.

В растворе ПАВ наблюдаются две тенденции:

1) Движение молекул ПАВ из объема на поверхность, приводящее к уменьшению поверхностной энергии и концентрированию ПАВ на поверхности.

2) Движение молекул ПАВ с поверхности в объем раствора (для выравнивания градиента концентрации), этот процесс ведет к увеличению энтропии.

Т.о. адсорбционное равновесие на поверхности раствор ПАВ–газ носит динамический характер.

Ленгмюр в 1932 г. был награжден Нобелевской премией по химии.

Модель Ленгмюра процессов адсорбции и десорбции ПАВ:

1. Молекулы ПАВ могут адсорбироваться из раствора только на свободных от ПАВ участках поверхности раствора.

2. Поверхностный (адсорбционный) слой ПАВ состоит только из одного слоя молекул ПАВ (монослой), поэтому теорию Ленгмюра называют теорией мономолекулярной адсорбции.

Исходя из этого получается, что удельная адсорбция имеет предельное значение Г_max. Введем понятие–доля поверхности, занятой молекулами ПАВ, θ, где:

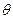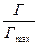= 6.3.1.

Соответственно доля свободной поверхности, которая будет равна:

1-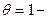

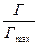
(доля свободной поверхности, которая доступна для адсорбции дополнительных молекул ПАВ).

Рассчитаем скорость адсорбции (моль/ м² с) :

ПАВ + свободная поверхность ↔ поверхность, занятая ПАВ

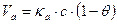6.3.2.

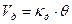6.3.3.

При равновесии 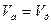6.3.4.

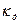=[моль/ м² с]

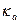=[л/ м² с ]

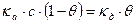
6.3.5.

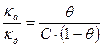6.3.6.

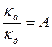
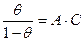6.3.7.

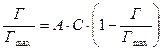6.3.9.

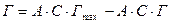6.3.10.

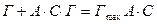6.3.11.

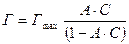6.3.12.

Рассмотрим два предельных:

1) В области малых концентраций, когда выполняется условие АС<<1.

Из уравнения Ленгмюра следует, что удельная адсорбция Г прямо пропорциональна объемной концентрации ПАВ С:

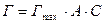6.3.13.

Т.е. начальный участок изотермы адсорбции представляет область Генри для поверхностного раствора ПАВ:

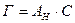6.3.14.

2) В области больших концентраций, когда ( пренебрегаем единицей):

,

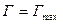т.е. достигается предельная максимальная адсорбция.

Для нахождения констант ( 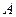и 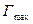) уравнение 6.3.12. приводят к линейной форме:

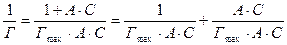6.3.15.

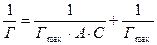6.3.16.

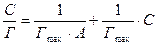6.3.17.