Химический потенциал и давление пара у искривленных поверхностей.
Рассмотрим малую сферическую каплю жидкой фазы α в фазе пара β. Используя уравнение для потенциала Гиббса для объемной фазы α при постоянных p и T, запишем:
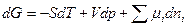. 4.4.1
, 
;
, 
.
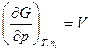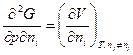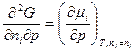Отсюда находим интересующую нас производную
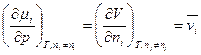, 4.4.2
где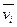 
– парциальный мольный объем i-го компонента.
В процессе образования кривизны в однокомпонентной (i=1) двухфазной (α, β) системе при T, s и ni = const получим:
4.4.3
4.4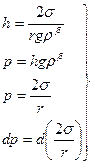.4 (см.§3)
Подставляя 4.4.4 в 4.4.3, получим:
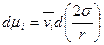, 4.4.5
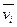в первом приближении можно считать постоянной.
Так как для воды при r = 10–7 м и σ = 73∙10–3 Н/м можно найти p = 1,5 МПа (15 атм). Эта величина мала по сравнению с внутренним давлением воды (≈103 МПа), и поэтому справедливо допущение, что в процессе искривления поверхности дополнительного сжатия жидкости не происходит.
Проинтегрируем выражение 4.4.5 в пределах от плоской поверхности (радиус r=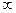 
) до искривленной поверхности (радиус r). 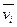вынесем за знак интегрирования, т.к. считаем ее постоянной.
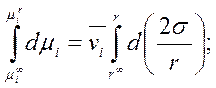
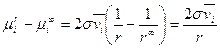, 4.4.6
где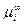 
– значение 
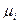вещества у плоской поверхности.
Из уравнения 4.4.6 следует, что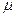 
в капле выше, чем у плоской поверхности. Но в состоянии равновесия 
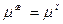, тогда, относя в уравнении 4.4.6 левую часть к пару, а правую – к жидкости, можно записать для идеальной системы
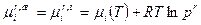. 4.4.7
Над плоской поверхностью
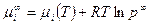. 4.4.8
Подставим 4.4.7 и 4.4.8 в выражение 4.4.6:
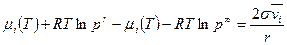, 4.4.9
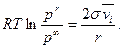4.4.10
Уравнение 4.4.10 называется уравнением Томсона (лорда Кельвина). Оно показывает, что давление насыщенного пара над каплей будет тем больше, чем больше σ и меньше радиус капли r.
Например, для воды при изменении радиуса от 10–5 см до 10–6 см давление увеличивается на 1 %. Это следствие уравнения Томсона (Кельвина) позволяет предсказать наблюдаемое явление изотермической перегонки, заключающееся в испарении малых капель и конденсации пара на более крупных каплях, а также на плоской поверхности.
Над вогнутым мениском жидкости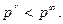 
В этом случае радиус кривизны меняет знак, и для сферического мениска получается аналогичное уравнение
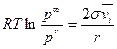. 4.4.11
Дата добавления: 2015-08-04; просмотров: 774;