Капиллярность. Капиллярное давление
При смачивании возникает искривление поверхности, изменяющее свойства поверхностного слоя. Существование избытка свободной энергии у искривленной поверхности приводит к так называемым капиллярным явлениям, своеобразие которых заключается в том, что давления в двух объемных фазах, разделенных искривленной поверхностью, оказываются различными в состоянии равновесия. Эти явления особенно существенны для дисперсных систем, характеризующихся большой кривизной (1/R).
Рассмотрим физический смысл капиллярных явлений на примере мыльного пузыря. Если в процессе выдувания пузыря открыть конец трубочки, то пузырь, находящийся на другом конце, начнет уменьшаться в размерах и втянется в трубку. Поскольку в этом обратном процессе воздух внутри пузыря сообщается с атмосферой, то для поддержания равновесного состояния давления изнутри должно быть больше внешнего. Если в этом опыте соединить трубку с манометром, то на нем устанавливается некоторая разность уровней, регистрирующая избыточное давление (∆Р) в объемной фазе газа с вогнутой стороны поверхности пузыря.
Для нахождения количественной зависимости между ∆Р и 1/R используем выражение для энергии Гельмгольца (2.3.9).
Рассмотрим две объемные фазы α и β, разделенные сферической поверхностью, находящиеся в состоянии равновесия при Т = const, например пузырек газа (α) в жидкой фазе (β) или каплю жидкости (α) в паровой фазе (β). В состоянии равновесия возможны вариации поверхности δs и объема δV пузырька без переноса вещества из одной фазы в другую, т.е. dni = 0. Пусть V увеличится на dV, а s – на ds. Тогда из выражения 2.3.9 останется:
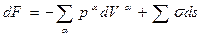 4.2.1
4.2.1
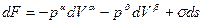 4.2.2
4.2.2
В состоянии равновесия при постоянстве общего объема системы, при Т = const, ni = const, dF = 0, т.е. над системой не совершается работа, и сама система работы не совершает.
Учитывая
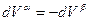 4.2.3.
4.2.3.
из выражения 4.2.2 получим:
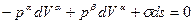 ,
,
 ,
,
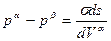 . 4.2.4
. 4.2.4
Таким образом,  .
.
Учитывая, что  и
и 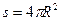 , где R – радиус кривизны, получаем:
, где R – радиус кривизны, получаем:
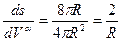 . 4.2.5
. 4.2.5
Подставляя выражение 4.2.5 в выражение 4.2.4, получим:
 . 4.2.6
. 4.2.6
Выражение 4.2.6 называется уравнением Лапласа–Юнга,а ∆р называют капиллярным давлением.
Уравнение 4.2.6 показывает, что разность давлений в объемных фазах возрастает с увеличением σ и уменьшением R. Величина R – это радиус кривизны поверхности натяжения.
Пример. Для капельки воды в фазе пара R = 10–5 см и ∆р ≈ 1,5 МПа (15 атм), т.е. давление внутри капли воды, равновесной с паром, оказывается на 15 атм выше, чем в фазе пара.
Независимо от агрегатного состояния фаз в состоянии равновесия давление с вогнутой стороны поверхности всегда больше, чем с выпуклой.
Уравнение 4.2.6 дает основу для экспериментального измерения σжг методом наибольшего давления пузырьков.
Дата добавления: 2015-08-04; просмотров: 1293;
