Приложение.

Дифференцирование радиуса-вектора точки в произвольном движении.

Дано: радиус – вектор 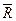произвольной точки. 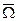- его абсолютная угловая скорость.

Абсолютная производная радиуса-вектора примет вид:

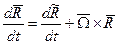( 5 ),

Здесь - 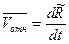, относительная скорость точки, характеризующая изменение длины радиуса-вектора;

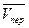- = , переносная скорость, учитывающая его вращение.

Продифференцировав ( 5 ) еще раз, получим:

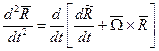( 6 )

Применив к ( 6 ) формальное правило дифференцирования вектора, стоящего в квадратной скобке, аналогично ( 5 ) можно получить выражение для абсолютного ускорения точки.

(дополнить, комментарий для составляющих абс. ускорения)[G1]

Если выявленные закономерности применить к соответствующим векторам выражения ( 3 ) и разрешить векторное уравнение относительно 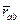, в котором присутствует наблюдаемая компонента 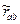, получим: