Электрокинематическая схема осевого акселерометра.
(вернуться к оглавлению)
Прибор, измеряющий «кажущееся» ускорение в проекции на ось x чувствительности.
 | |||||
| |||||
 |
Рис. 8. Электрокинематическая схема акселерометра
Понятние осевой – чувствительный элемент массы может двигаться поступательно (по оси х)
Позициями на рис. обозначены:
1. ЧЭ с массой - m
2. Подвес массы – узел подвеса (устройство, обеспечивающее ЧЭ необходимым количеством степеней свободы относительно корпуса 3)
3. Корпус
4. Датчик положения (Кдп), смещения ЧЭ относительно корпуса (преобразователь механического перемещения в электрический сигнал)
5. Усилитель (Ку)
6. Задатчик силы воздействия на ЧЭ со стороны упругих связей: (Fx=Cxx), где Сx – жесткость упругих элементов.
7. Устройство демпфирования колебаний массы ЧЭ: Fд=Kдx, где Kд -коэффициент демпфирования.
Уравнение статического равновесия ЧЭ осевого акселерометра в общем виде в соответствии с законами кинетостатики может быть представлено:
∑Fy=0; m (gy+ay)=Ry ; Ry=Cy*Δy
∑Fz=0; m(gz+az)=Rz ; Rz=Cz*Δz
∑Fx=0; Fи+Fу+Fg = Fвнешн.
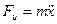 ;
;
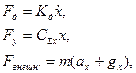
 .
.
Уравнение движения ЧЭ относительно оси Х примет вид:
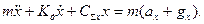 , [H] .
, [H] .
Это же уравнение в форме удельных сил:
 , [м/с2],
, [м/с2],
где: - 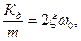
- 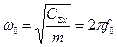 - собственная круговая частота недемпфированных колебаний;
- собственная круговая частота недемпфированных колебаний;
- 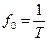 [1/c], [Гц];
[1/c], [Гц];
- ξ – относительный коэффициент демпфирования.
Возникающие колебания будут состоять из свободных и вынужденных.
Вид свободных колебаний определяется видом корней характеристического уравнения:
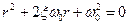 .
.
При чисто мнимых корнях - r1 и r2, что будет иметь место при ξ=0, будет чисто колебательный процесс без затухания (консервативная система).
Полный запас энергии системы остается постоянным:
Ек + П =Constant,
где - Eк=mV2/2,
- П=Сx2/2.
На рис. 9. Иллюстрируется процесс незатухающих колебаний ЧЭ такой консервативной системы.
На рис. 10. Показан переходный процесс для случая 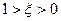 .
.

|
|


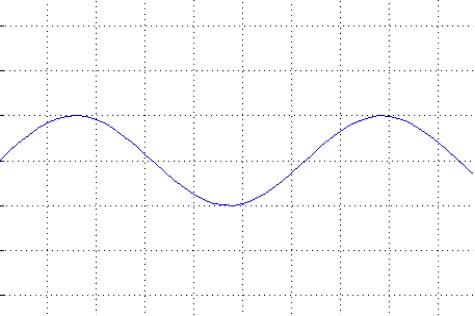
Рис.9


|
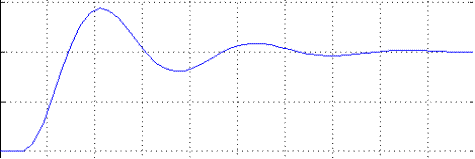
Рис. 10.
Затухающие колебания, наблюдаемые в системе.
Дата добавления: 2015-08-04; просмотров: 1720;

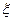 <1
<1