Определение потерь напора в прямой цилиндрической трубе
Казань – 2008
Цель работы: 1) определение потерь напора 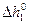 непосредственно из опыта при различных скоростях движения воды;
непосредственно из опыта при различных скоростях движения воды;
2) определение потерь напора по длине 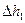 расчетным путем; 3) сравнение полученных опытных значений с вычисленными.
расчетным путем; 3) сравнение полученных опытных значений с вычисленными.
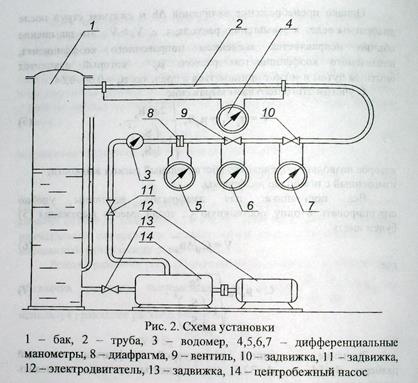
Описание установки: (рисунок на последней странице) установка состоит из центробежного насоса 14, бака 1, трубопровода, включающего прямую горизонтальную круглую стальную трубу 2, регулировочных задвижек 11 и 13. Потери напора в трубе измеряются дифференциальным манометром 4, присоединенным к начальному и конечному сечениям исследуемого участка трубы с помощью пьезометрических колец и импульсных трубок. Расход протекающей через трубопровод воды регулируется задвижкой 11 и определяется с помощью водомера 3 и секундомера.
Сущность работы: гидравлические потери напора по длине (путевые потери) при течении жидкости в прямой трубе обусловлены трением слоев жидкости друг о друга и о стенки канала и определяются по формуле Дарси-Вейербаха:
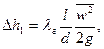
Где 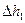 - величина потерянного напора на прямом участке трубопровода длиной
- величина потерянного напора на прямом участке трубопровода длиной 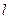 , м;
, м; 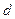 - внутренний диаметр трубы, м;
- внутренний диаметр трубы, м; 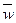 - средняя скорость потока, м/с;
- средняя скорость потока, м/с; 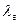 - коэффициент гидравлического трения.
- коэффициент гидравлического трения.
Как показывают опыты, коэффициент гидравлического трения зависит от численного значения критерия Рейнольдса и относительной шероховатости стенки трубы, т.е.: 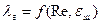 . Здесь
. Здесь 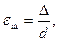 где
где 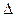 - абсолютная шероховатость, т.е. средняя высота неровностей на стенке трубы. Значение коэффициента
- абсолютная шероховатость, т.е. средняя высота неровностей на стенке трубы. Значение коэффициента 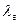 определяется обычно по эмпирическим формулам, полученным для различных областей сопротивления по кривой Никурадзе.
определяется обычно по эмпирическим формулам, полученным для различных областей сопротивления по кривой Никурадзе.
1. Для ламинарного режима течения, Re<2320, коэффициент 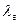 для всех труб независимо от их шероховатости определяется из точного решения задачи о ламинарном течении жидкости в прямой круглой трубе по формуле Пуазейля:
для всех труб независимо от их шероховатости определяется из точного решения задачи о ламинарном течении жидкости в прямой круглой трубе по формуле Пуазейля:
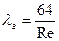 .
.
2. В узкой области 2320<Re<3000 наблюдается скачкообразный рост коэффициента трения. Эта область характеризуется неустойчивым характером течения. Здесь вероятнее турбулентный режим и правильнее всего использовать формулу для области 3, но можно воспользоваться тривиальной формулой:
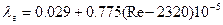
3. В области гидравлически гладких труб при 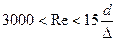 толщина ламинарного слоя у стенки
толщина ламинарного слоя у стенки 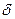 больше абсолютной шероховатости стенок
больше абсолютной шероховатости стенок 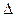 . Влияние выступов шероховатости, омываемых безотрывным потоком, практически не сказывается, и коэффициент сопротивления вычисляется на основании обобщения опытных данных по эмпирическим соотношениям по формуле Блаузиуса:
. Влияние выступов шероховатости, омываемых безотрывным потоком, практически не сказывается, и коэффициент сопротивления вычисляется на основании обобщения опытных данных по эмпирическим соотношениям по формуле Блаузиуса:
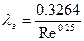 .
.
4. В диапазоне чисел Рейнольдса 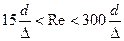 наблюдается переходная область от гидравлически гладких труб к шероховатым. Коэффициент сопротивления в этом случае рассчитывается по формуле Альтшуля:
наблюдается переходная область от гидравлически гладких труб к шероховатым. Коэффициент сопротивления в этом случае рассчитывается по формуле Альтшуля:
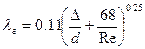
5. При 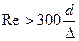 толщина ламинарного слоя у стенки
толщина ламинарного слоя у стенки 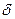 достигает своего минимального значения. Коэффициент сопротивления рассчитывают по формуле Шифринсона:
достигает своего минимального значения. Коэффициент сопротивления рассчитывают по формуле Шифринсона:
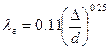
Порядок проведения опытов: открывается задвижка 13 и закрывается задвижка 11. При условии наличия воды в баке 1 пускается насос. Полностью открывается задвижка 11. Измеряется разность давлений по дифманометру 4, время прохождения определенного объёма воды, указанного преподавателем и измеренного водомером 3. С помощью ртутного термометра измеряется температура воды.
Следующие опыты проводят при меньших расходах в той же последовательности. Об изменениях расхода можно судить по показаниям дифманометра. Разница показаний дифманометра от опыта к опыту должна быть достаточно заметной. Всего проводится 4-5 опытов.
Таблица измеренных и рассчитанных величин:
| № | 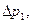 Па Па
| 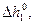 м м
| V, л | t, с | 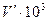 , м³/с , м³/с
| 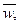 м/с м/с
| Re | 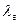
| 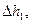 м м
|
| 0,0010 | 0,5 | 0,22 | 0,036 | 0,0066 | |||||
| 0,0081 | 2,12 | 0,93 | 0,031 | 0,1013 | |||||
| 0,0204 | 3,57 | 1,56 | 0,029 | 0,2667 | |||||
| 0,0387 | 4,76 | 2,08 | 0,029 | 0,4742 | |||||
| 0,0510 | 5,56 | 2,43 | 0,029 | 0,6472 | |||||
| 0,0622 | 6,25 | 2,73 | 0,029 | 0,8168 | |||||
| 0,0785 | 7,14 | 3,12 | 0,029 | 1,0669 | |||||
| 0,0888 | 7,69 | 3,36 | 0,029 | 1,2373 |
Расчёты:
Рассчитаем 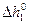 для всех опытов:
для всех опытов:
1) 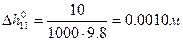
2) 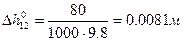
3) 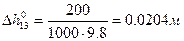
4) 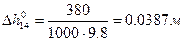
5) 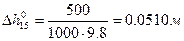
6) 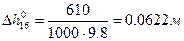
7) 
8) 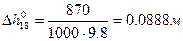
Рассчитаем теперь объёмный расход воды:
1) 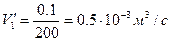
2) 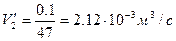
3) 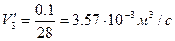
4) 
5) 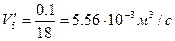
6) 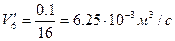
7) 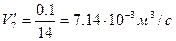
8) 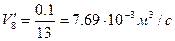
Живое сечение потока 
Рассчитаем скорость потока:
1) 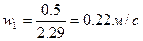
2) 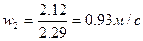
3) 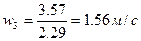
4) 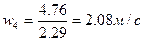
5) 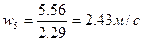
6) 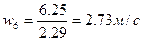
7) 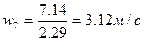
8) 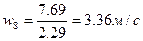
Рассчитаем коэффициент Рейнольдса:
1) 
2) 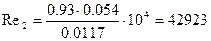
3) 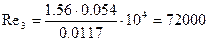
4) 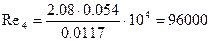
5) 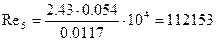
6) 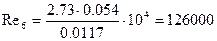
7) 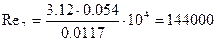
8) 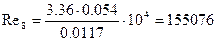
Рассчитаем коэффициент гидравлического трения:
1) 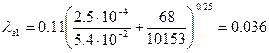
2) 
3) 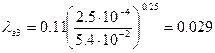 Для последующих опытов, значение данного коэффициента будет таким же, как и для опыта 3.
Для последующих опытов, значение данного коэффициента будет таким же, как и для опыта 3.
Рассчитаем значение потерь напора по длине:
1) 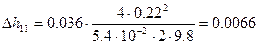
2) 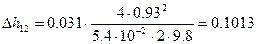
3) 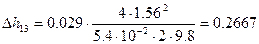
4) 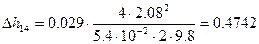
5) 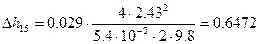
6) 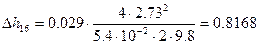
7) 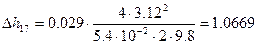
8) 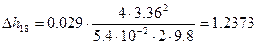
Вывод: в результате проделанной работы, мы определили потери напора 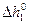 непосредственно из опыта при различных скоростях движения воды. Также мы рассчитали значение
непосредственно из опыта при различных скоростях движения воды. Также мы рассчитали значение 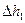 расчётным путем и сравнили его с опытными данными.
расчётным путем и сравнили его с опытными данными.
| <== предыдущая лекция | | | следующая лекция ==> |
| Упражнение 2. Исследовать зависимость напряжения на выходе выпрямителя от силы выпрямленного тока. | | | Экспериментальная демонстрация уравнения Бернулли |
Дата добавления: 2015-08-01; просмотров: 3667;
