Указания к решению задачи
При недостаточности данных гидрометрических наблюденийна реке Впараметры кривой обеспеченности гидрологических характеристик стока или уровней воды необходимо привести к многолетнему периоду используя данные реки-аналога (рек-аналогов) и методы парной или множественной регрессии. При этом необходимо выполнить следующие условия:
- река-аналог или реки-аналоги должны отвечать указанным ниже требованиям;
- число совместных наблюдений на рассматриваемой реке и реках-аналогах должно быть не менее 6 лет при одном аналоге, и не менее 10 лет при двух и более аналогах;
- коэффициент корреляции между стоком в приводимом пункте и пунктах рек-аналогов должен быть не менее 0,7;
Основными требованиями, предъявляемыми к реке-аналогу, являются:
- географическая близость расположения водосборов;
- однородность условий формирования стока реки-аналога и исследуемой реки: сходство климатических условий, однотипность почв и грунтов, гидрогеологических условий, близкие степени озерности, залесенности, заболоченности и распаханности);
- отсутствие факторов, существенно искажающих естественный речной сток (регулирование стока, сбросы и изъятия воды и др.).
Мерой тесноты связи между двумя статистическими рядами служит коэффициент корреляции, определяемый по формуле:
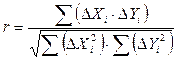 , (5)
, (5)
где Δ Xi = Хi – Xc; Δ Yi = Yi – Yc;
Xi и Yi – соответствующие друг другу (по годам) ежегодные расходы воды с количеством членов n лет;
Хс , Yc – средние арифметические значения рядов, т.е. Хс = ∑ Хi / n; Yc = ∑ Yi / n.
Результаты расчета сведены в табл. 2.
Уравнение регрессии, которое предполагается использовать для удлинения ряда по данным одной реки-аналога, имеет вид:
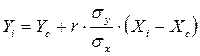 (6)
(6)
где σу, σх – средние квадратические отклонения, определяемые по формулам:
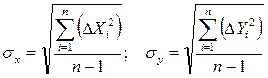 (7)
(7)
При использовании нескольких рек-аналогов (j) удлинение гидрологического ряда производится по уравнению множественной линейной регрессии:
Yi = K0 + K1* (X1)i + K2 * (X2)i + … + Kj * (Xj)i,
где K1…Kj – значения стока или уровней воды в реках-аналогах (1…j);
K0 – свободный член;
K1…Kj – коэффициенты уравнения регрессии.
Коэффициенты и свободный член этого уравнения определяют методом наименьших квадратов (МНК).
Статистическая обработка удлиненного ряда наблюдений за стоком на реке В и определение параметров кривой обеспеченности проводится в соответствии с указаниями, изложенными в задаче 1.
При использовании графического метода удлинения ряда наблюдений по данным табл. 2 строится график связи между соответствующими расходами воды. Недостающие значения расхода воды для рассматриваемой реки определяются приближенно по этому графику. При этом целесообразно построить такие графики для нескольких рек-аналогов, из которых для удлинения ряда принимают график, имеющий наибольший коэффициент корреляции. Этот метод допускается применять на начальных этапах проектирования гидротехнических сооружений.
Пример
Исходные данные:
Для выбранного варианта из прил. 1 используем два ряда параллельных наблюдений по реке А и В продолжительностью 11 лет (1992 – 2002 гг.).
1. Установлено, что река А может являться рекой-аналогом, так как отвечает требованиям, предъявляемым к рекам-аналогам, и имеет более длительный период гидрометрических наблюдений по сравнению с рекой В.
Для приведения кратковременных наблюдений на реке В к многолетнему периоду применим метод парной регрессии.
Результаты расчета параметров, необходимых для определения коэффициентов корреляции и регрессии, сведены в табл. 2.
Вычислим средние значения:
Хс = ∑Хi / 11 = 3801 / 11 = 345,5 м3/с;
Yc = ∑ Yi / 11 = 2245/ 11 = 204,1 м3/с.
Отклонения от средних арифметических значений будут равны:
Δ Xi = Хi – Xc; Δ Yi = Yi – Yc.
Коэффициент корреляции определим по формуле (5):
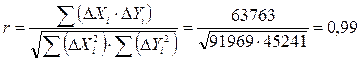
Таблица 2
| Годы | Xi, м3/с | Yi, м3/с | ΔXi, м3/с | ΔYi, м3/с | ΔXi *ΔYi, | ΔXi2 | ΔYi2 |
| 28.5 -145.5 0.5 145.5 126,5 -16,5 -43,5 131,5 -100,5 -85 -117,5 | -13.1 -80.1 -11.1 76.9 110,9 -31,1 -53,1 103,9 -67,1 -1,1 -35,1 | -373 -6 | |||||
| - | ∑Xi = 3801 | ∑Yi = 2245 | - | - | ∑ΔXi *ΔYi =63763 | ∑ΔXi2 =91969 | ∑ΔYi2 =45241 |
Для удлинения ряда воспользуемся уравнением регрессии (6), в котором:
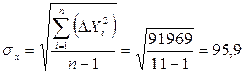
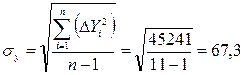
Таким образом, выполнено условие возможности применения метода парной регрессии для удлинения данного гидрологического ряда, т.е.: коэффициент корреляции r > 0.7.
2. Прямую связи расходов рек А и В построим по двум значениям Xi, охватывающим весь ряд наблюдений на реке А:
X1 = 600 м3/с. Эта величина больше Xmax = 576 м3/с.
Х2 = 150 м3/с. Эта величина меньше Хmin = 185 м3/с.
Y1 = 204,1 + 0,99 * (67,3/95,9) * (600 – 345,5) = 379,7 м3/с;
Y2 = 204,1 + 0,99 * (67,3/95,9) * (150 – 345,5) = 69,2 м3/с.
После построения прямой связи, нанесем на график точки с соответствующими значениями Xi и Yi (табл. 2), которые должны находиться рядом с прямой (рис. 1).
3. По уравнению регрессии (6) определим 20 недостающих расходов воды (до n = 31) в реке В для соответствующих значений расходов воды в реке А. Определенные значения расходов воды в реке В, заключенные в скобках, приводятся в отчете.
Река (В), Yi , м3/с 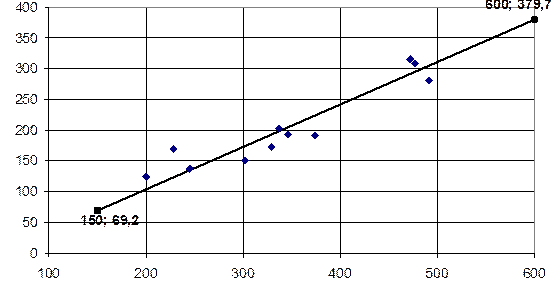
Река (А), Xi , м3/с
Рис. 1. Прямая связи расходов рек А и В. (Точками показаны расходы воды за 11 лет параллельных наблюдений).
Литература
1. СП 33-101-2003. Определение основных расчетных гидрологических характеристик. Госстрой России. М., 2004.
2. Пособие по определению расчетных гидрологических характеристик». - Л., Гидрометеоиздат, 1984.
3. Ресурсы поверхностных вод СССР. Ч. 1-2. Л., Гидрометеоиздат, 1972-75.
4. Железняков Г.В. и др. Гидрология, гидрометрия и регулирование стока. – М., Колос, 1984.
5. Гидрология и гидротехнические сооружения: Уч. для Вузов / Г.Н. Смирнов и др. М., Высш. шк., 1988.
6. СП 11-103-97. Инженерно-гидрометеорологические изыскания. Госстрой России. М., 1998.
7. СНиП 2.04.03 - 85. Канализация. Наружные сети и сооружения. М., 1986.
8. Андреев О.В. и др. Русловые и гидравлические расчеты при проектировании переходов через водотоки. Уч. пособие. М., 1989.
Дата добавления: 2015-08-01; просмотров: 903;
