Указания к решению задачи. Поведение случайных величин, которые составляют заданный гидрологический ряд наблюдений, можно охарактеризовать тремя параметрами:
Поведение случайных величин, которые составляют заданный гидрологический ряд наблюдений, можно охарактеризовать тремя параметрами:
- средним арифметическим значением;
- коэффициентом вариации;
- коэффициентом асимметрии.
Среднее арифметическое значение ряда:
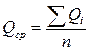 (1)
(1)
где: Qi – максимальный расход весеннего половодья, м3/с;
n – количество членов ряда.
Коэффициенты вариации и асимметрии определяются в соответствии с СП 33-101-2003 методами моментов и наибольшего правдоподобия.
1. Метод моментов. Коэффициент вариации Сv характеризует меру изменчивости членов ряда относительно среднего арифметического значения и определяется по формуле (при Сv < 0.6):
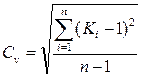 , (2)
, (2)
где Ki – частное от деления i-го члена ряда на среднее арифметическое этого ряда, т.е. 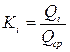 .
.
Коэффициент асимметрии Сs характеризует отличие по величине и количеству положительных (больше средних) и отрицательных (меньше средних) отклонений от среднего арифметического значения ряда. Для симметричных рядов (нормальное распределение ежегодных вероятностей превышения значений ряда) эти отклонения повторяются одинаково часто, поэтому Cs = 0. Для несимметричных рядов Cs ≠ 0, а коэффициент асимметрии определяется по формуле (при Сs < 1,0):
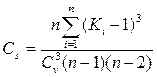 (3)
(3)
Расчеты по определению статистических характеристик сводятся в табл. 1. В верхней строке этой таблицы указана точность, с которой необходимо определить соответствующие величины.
Для проверки правильности определения среднего значения сравниваем суммы положительных и отрицательных значений ∑(Ki - 1). Они должны отличаться один от другого не более чем на 5%.
2. Метод наибольшего правдоподобия. Для оценки коэффициентов вариации и асимметрии этим методом необходимо предварительно определить величины статистик:
 (4)
(4)
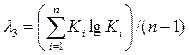
Результаты расчета, необходимые для определения этих статистик, сводятся в табл. 1. По рассчитанным значениям статистик по одной из номограмм (прил. 2) определяют характеристики ряда: Cv, Cs/Cv и Cs.
3. После определения параметров статистического ряда этими методами, по таблицам прил. 3 находится ордината кривой трехпараметрического гамма-распределения ежегодных вероятностей превышения значений гидрологической характеристики (кривой обеспеченности) для заданной 1% обеспеченности К1%. По ней вычисляем максимальный расход воды заданной обеспеченности Q1% = К1% * Qср
Пример
Исходные данные:
Ряд наблюдений за максимальным расходом воды в реке А продолжительностью n =31 год для выбранного варианта (см. прил. 1).
1. Вычислим статистические характеристики ряда наблюдений, предварительно выполнив расчеты по форме табл.1
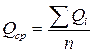 =11378 / 31 = 367 м3/с.
=11378 / 31 = 367 м3/с.
+ ∑ (Кi - 1) = 3.26
- ∑ (Ki - 1) = - 3.25
Суммы положительных и отрицательных значений ∑(Ki – 1) отличаются менее чем на 5%.
а) метод моментов:
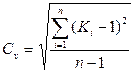
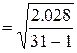 =0.26
=0.26
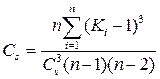 =
= 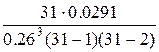 =0.059
=0.059
б) метод наибольшего правдоподобия:

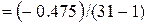 =- 0,016
=- 0,016

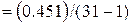 =0,015
=0,015
По номограмме (прил. 2) определим:
Cv = 0.26, Cs / Cv = 0.4, Cs = (Cs/Cv) * Cv = 0.4 * 0.26 = 0.1
2. По таблицам прил. 3 определим ординаты теоретических кривых обеспеченности и величины максимальных расходов воды 1% вероятности превышения. При Cs / Cv < 0.5 для определения ординат кривых обеспеченности используется таблица прил. 3 при Cs / Cv = 0.5.
а) метод моментов (Qср = 367 м3/с, Cv = 0,26, Cs = 0,059):
К1% = 1, 60;
Q1% = К1% * Qср = 1,60 * 367 = 587 м3/с.
б) метод наибольшего правдоподобия (Qср = 367 м3/с, Cv = 0.26, Cs = 0,1):
К1% = 1, 60;
Q1% = К1% * Qср = 1,60 * 367 = 587 м3/с.
3. В качестве расчетного максимального расхода принимаем наибольшее значение из вычисленных методами моментов и наибольшего правдоподобия. Таким образом, Q1% = 587 м3/c.
Таблица 1
| m | Qi в убывав. порядке | Ki | Ki -1 | (Ki-1)2 | (Ki-1)3 | p, % | lg Ki | Ki*lg Ki |
| Точность | 0,01 | 0,01 | 0,001 | 0,0001 | 0,1 | 0,001 | 0,001 | |
| … … | …. … | 1,57 1,43 … … 0,54 0,50 | 0,57 0,43 … … -0,46 -0,50 | 0,325 0,185 … … 0,212 0,250 | 0,1852 0,0795 … … -0,0973 -0,1250 | 3,1 6,3 … … 93,8 96,9 | 0,196 0,155 … … -0,268 -0,301 | 0,308 0,222 … … -0,145 -0,150 |
| ∑Qi= =11378 | + 3.26 - 3.25 | ∑ = =2.028 | ∑= =+0.0291 | ∑= = -0.475 | ∑= =0.451 |
Дата добавления: 2015-08-01; просмотров: 759;
