Температурное поле
Температурным полем называется совокупность значений температур в данный момент времени во всех точках рассматриваемого пространства, занятого теплом.
Если температура поля с течением времени t изменяется, то оно называетсянестационарным и описывается уравнением:
T = f(x,y,z,t), (1)
где x,y,z – координаты точки поля.
Если же температура в каждой точке поля с течением времени t, остается неизменной, то такое температурное поле называетсястационарным. Температура, в этом случае, является функцией только пространственных координат
T = f(x,y,z), ¶T/¶t = 0. (2)
В каждый момент времени в температурном поле можно выделить поверхности, имеющие одинаковые температуры. Такие поверхности называются изотермическими. В стационарном температурном поле изотермические поверхности с течением времени не меняют свой вид и расположение, в то время как в нестационарном поле они со временем изменяются.
Температурный градиент
Одной из характеристик температурного поля является температурный градиент, представляющий собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. На рис.4.1. изображены изотермические поверхности, температуры которых отличаются на DТ.
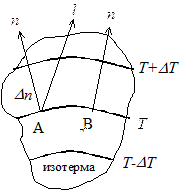
Рис. 1. К понятию температурного градиента
Из рисунка видно, что интенсивность изменения температуры по разным направлениям (из точки А лучи п и l) неодинакова. Наибольшая разность температур на единицу длины наблюдается в направление нормали п к изотермической поверхности в точке А, так как расстояние между соседними изотермами Dn при этом меньше, чем в точке В.
Предел отношения изменения температуры DТ к расстоянию между изотермами по нормали Dn, когда Dn стремится к нулю, называетсятемпературным градиентом:
grad T = lim(DT/Dn)Dn®0 = (¶T/¶n)no. (3)
В общем случае для различных точек одной и той же изотермической поверхности (например, для точек А и В) градиент температуры различен не только по направлению, но и по величине. За положительное направление градиента принято направление возрастания температур.
Основы теплового расчета
Несмотря на многообразие конструкций и принципов работы теплообменных аппаратов, процессы теплообмена в них подчиняются общим закономерностям, а основные положения методики их расчета могут быть рассмотрены в общей постановке.
До недавнего времени расчет теплообменных аппаратов приводился только для стационарных режимов, и при этом в основном решались две задачи:
1. Для заданных параметров на входе и выходе из аппарата и типе теплообменной поверхности определить требуемую площадь поверхности теплообмена и произвести его конструктивную разработку. Это есть проектный расчет.
2. Для реально существующего аппарата при заданных параметрах потоков на входе определить количество передаваемой теплоты и параметры потоков на выходе из аппарата. Это задача проверочного расчета.
К этим двум задачам можно добавить третью, так называемый оптимальный расчет теплообменного аппарата. Решение этой задачи возможно благодаря использованию ЭВМ. Суть этой задачи сводится к расчету оптимального теплообменника по выбранному критерию.
Тепловой расчет теплообменных аппаратов базируется на уравнениях теплового баланса и теплопередачи.
Решение нестационарных задач теплообмена возможно только при использовании математических моделей, записанных на основе моделей структуры потоков теплоносителей.
Проектный расчет теплообменного аппарата
Задачей проектного расчета является определение геометрических размеров и режима работы теплообменника, необходимого для отвода или подвода заданного количества теплоты к теплоносителю.
При проектном расчете задают:
1. Тип аппарата и общие геометрические характеристики поверхности теплообмена (размеры труб, оребрения, толщина стенок и др.).
2. Параметры теплоносителей на входе и выходе из аппарата (температура, давление и т.д.)
3. Тепловую мощность аппарата Q или расход сред.
Взаимность изменений температур теплоносителей определяется условием теплового баланса, которое для бесконечно малого элемента теплообменника имеет вид:
– G1Cp1dT1 = G2Cp2dT2. (4)
Здесь G1, G2, Cp1, CP2 – расходы и теплоемкости теплоносителей 1 и 2, T1 и Т2 – их температуры в произвольном сечении аппарата. Уравнение теплового баланса для всего аппарата получается путем интегрирования уравнения (4.4) и имеет вид:
Gl Cpl (Tk1–Th1) = G2 Cp2 (Th2–Tk2), (5)
где Тh1 и Th2, Tk1 и Tk2 – начальные и конечные температуры теплоносителей.
Уравнение (4.5) содержит две неизвестные: G1 или G2 и Tk1 или Tk2. Следовательно, это уравнение является неопределенным. Общий прием решения этих задач заключается в использовании метода последовательных приближений, состоящего в том, что в начале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется до получения результатов с желаемой степенью точности.
Проверочный расчет теплообменного аппарата
Целью проверочного расчета теплообменного аппарата заданной конструкции является определение его мощности и температур потоков на выходе Тk1, Tk2 при заданных площадях поверхности теплообмена F, расхода сред G1, G2 и их температурах на входе Тh1 и Тh2.
Математические модели теплообменников
Обычно принимают, что движение потоков теплоносителя и хладоагента характеризуется гидродинамическими моделями идеального смешения, идеального вытеснения, ячеечной моделью ОДМ или их комбинацией.
Если гидродинамическая структура потоков в теплообменном аппарате соответствует модели идеального смешения, то во всем потоке происходит полное смешение молекул потока. В таком случае любое изменение температуры потока на входе в зону идеального смешения мгновенно распространяется по всему объему зоны.
Гидродинамическая структура потоков теплоносителя, соответствующая модели идеального смешения, имеет место в теплообменных аппаратах с изменением агрегатного состояния потоков – в конденсаторах, кипятильниках, испарителях. Уравнение, описывающее изменение температуры для теплообменника в зоне идеального смешения, имеет вид:
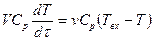, (6)
где V – объем зоны идеального смешения; v – объемная скорость; Твх, Т – температура потока на входе и в зоне идеального смешения; Ср – теплоемкость потока; t – время.
Условие физической реализуемости модели идеального вытеснения выполняются в случае поршневого потока, когда предполагается, что в направлении его движения смещение полностью отсутствует, а в направлении, перпендикулярном движению, происходит идеальное смешение. Гидродинамическая структура потоков, соответствующая модели идеального вытеснения, характерна для движения потоков в трубном пространстве кожухотрубчатых теплообменников различных конструкций, а также для теплообменного аппарата типа «труба в трубе».
Уравнение, описывающее изменение температуры в зоне идеального вытеснения, имеет вид:
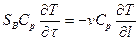, (7)
где Sb – сечение зоны идеального вытеснения; l – координата длины аппарата.
Диффузионная модель гидродинамической структуры потоков соответствует такому движению потоков, когда в направлении его движения существует продольное смещение, а перпендикулярном направлении предполагается наличие идеального смешения.
Диффузионная модель значительно лучше, чем модель идеального вытеснения, описывает гидродинамические условия в реальных кожухотрубчатых теплообменниках. Уравнение, характеризующее изменение температуры по длине зоны, имеет вид:
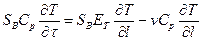, (8)
где ет – коэффициент продольного переноса теплоты.
Температуры потоков в теплообменных аппаратах могут изменяться в каждой точке потока не только в результате его движения, но также из-за теплообмена с окружающей средой или за счет источника теплоты. Интенсивность источника теплоты записывается следующим образом:
V qT = F*K*DT, (9)
где F – поверхность теплообмена, отнесенная к единице объема; К – коэффициент теплопередачи; DТ – разность температур.
Уравнения (4.6) и (4.7) для температур потока с учетом источника теплоты в потоке имеет вид:
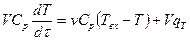;(10)
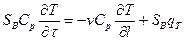. (11)
Учитывая (4.9) и зная, что V = S*L из (4.11) получим:
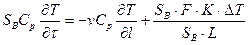или
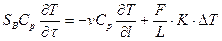. (12)
Аналогично для ДДМ с учетом (4.9) имеем:
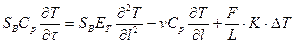. (13)
Для описания гидродинамической структуры потоков в реальных теплообменных аппаратах используются комбинированные модели движения потоков: ячеечная модель; модель идеального смешения с застойной зоной; модель идеального смешения с байпасом; последовательное соединение двух моделей МИС и МИВ. Применение таких моделей для описания гидродинамической структуры потоков позволяет описать изменение профиля температур как по длине, так и в объеме теплообменного аппарата.
Теплообменник типа «перемешивание-перемешивание»
Математическая модель такого теплообменника (рис.4.2) представляет собой систему уравнений типа (4.7), записанных для теплоносителя и хладоагента:
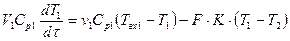
, (14)
где T1 – T2 = DT, при этом T1 и T2 имеют постоянные значения в каждой точке объема идеального перемешивания V1 и V2; Твх1, Твх2 – температуры первичного и вторичного теплоносителей на входе в аппарат; Тк1 = Т2 и Тк2 = Т2 – конечные температуры первичного и вторичного теплоносителей. Величина FK(T1 – T2) имеет знак «минус» в уравнении описания потока теплоносителя, который отдает тепло, и знак «плюс», если тепло воспринимается теплоносителем.
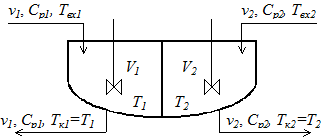
Рис. 2. Схематическое изображение теплообменника типа «перемешивание-перемешивание»
Теплообменник типа «перемешивание-вытеснение»
Математическая модель такого теплообменника (рис.4.3) включает уравнение модели идеального перемешивания для потока теплоносителя и уравнение модели идеального вытеснения для хладоагента:
;
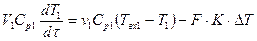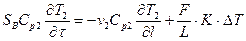, (15)
где DT = T1 – T2 при этом значения T1 остается одинаковыми в каждой точке объема идеального перемешивания, а Т2 изменяются по длине зоны идеального вытеснения.
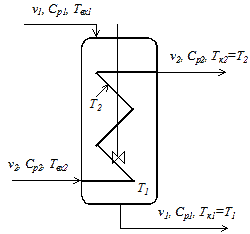
Рис. 3. Схематическое изображение теплообменника типа «перемешивание - вытеснение»
Теплообменник типа «вытеснение-вытеснение»
Рассмотрим моделирование широко распространенного в химической технологии теплообменника «труба в трубе», структура потоков которого соответствует модели «вытеснение – вытеснение» (рис.3.1).
Рис.4. Схема теплообменника типа «труба в трубе»
Это так называемый прямоточный теплообменник, для которого модель имеет вид:
;
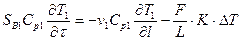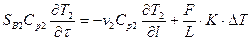, (16)
где DT = T1 – T2, при этом Т1 и Т2 изменяются по длине соответствующих зон идеального вытеснения. Цель работы: построить математическую модель и рассчитать теплообменный аппарат с известной структурой потоков.
Дата добавления: 2015-08-01; просмотров: 12294;