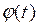Математическое моделирование однофазных потоков

Основой математической модели любого химико-технологического процесса, в котором происходит перемещение вещества, является математическое описание структуры потоков.

Гидродинамика реальных потоков настолько сложна, что на основании теоретических предположений уравнения в общем виде можно вывести только для однофазных потоков, причем решение их известно лишь для частных случаев. Поэтому, при составлении математических описаний приходится использовать приближенное представление о структуре потоков, основанное на том, что структура движущийся технологической среды характеризуется степенью перемешивания частиц. Основной показатель степени перемешивания - время пребываний частицы в аппарате.

Известно, что время пребывания частиц потока в аппарате является непрерывной случайной величиной. Основной ее характеристикой служат функции распределения времени пребывания: дифференциальная и интегральная. По виду функции распределения с некоторым приближенным значением можно судить о внутренней структуре потока.

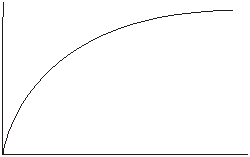
Дифференциальная функция распределения времени пребывания :

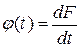, (1).

которая показывает долю потока за время от ti-1до ti (рис. б).

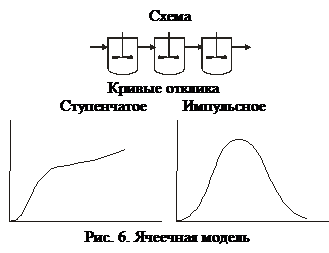
При разработке математической модели структуры потоков на практике прибегают к использованию так называемых типовых моделей. Наиболее распространенными из них являются: модель идеального смешивания (МИП), модель идеального вытеснения (МИВ), ячеечная модель (ЯМ), однопараметрическая диффузионная модель (ОДМ).

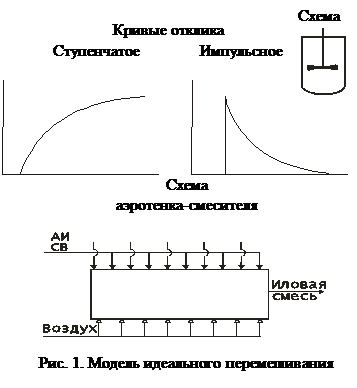
На практике иссследование структуры потоков ведется с помощью веществ - трассеров. Трассеры вводят в аппарат и на выходе получают кривую отклика. существуют два способа ввода трассеров в аппарат:

- ступенчатый;

- импульсный.

Для типовых моделей кривые отклика известны.

По кривым отклика можно получить функции распределения времени пребывания, которая может быть охарактеризована числовыми характеристиками – моментами. Обычно используют размерные моменты нулевого M₀, первого M₁ и второго M₂ порядков. Общая формула для нахождения размерных моментов:

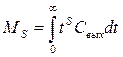, (2)

где S – порядок момента, С_вых – дифференциальная функция распределения времени пребывания. Тогда

, , .

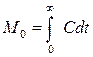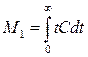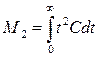Момент нулевого порядка равен площади, ограниченной кривой распределения. Момент первого порядка характеризует среднее время пребывания элемента потока в аппарате, момент второго порядка – дисперсию времени пребывания. От моментов для кривой отклика путем несложных преобразований можно перейти к приведенным моментам. Общая формула для приведенных моментов

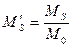. (3)

Тогда , , .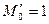

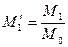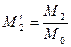Безразмерный момент вычисляется по формулам

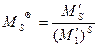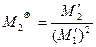, . (4)

Безразмерный момент второго порядка связан в свою очередь с параметрами ОДМ и ЯМ следующим образом:

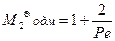, (5)

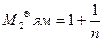, (6)

где Pe = U*L/D_x – критерий Пекле (где U – линейная скорость потока; L – длина аппарата).

Следовательно, вычислив безразмерный момент второго порядка, можно найти коэффициент продольного перемешивания D_x и количество ячеек n.

Модель идеального перемешивания:

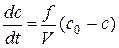(7)

предполагает, что поступающий в аппарат поток мгновенно распределяется по всему объему вследствие полного перемешивания. При этом концентрация вещества во всех точках аппарата и в выходном потоке одинакова.

Модель идеального вытеснения:

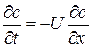(1.3)

используется при описании аппаратов, работающих по принципу вытеснения.

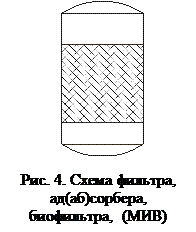
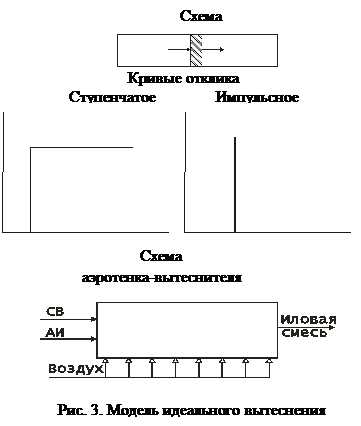Биофильтры, адсорберы также относятся к аппаратам с идеальным вытеснением (рис. 4).

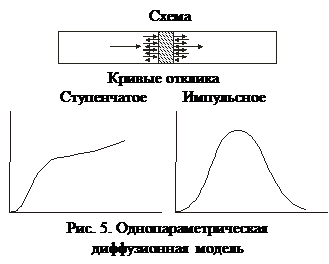
Однопараметрическая диффузионная модель:

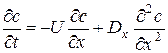(1.4)

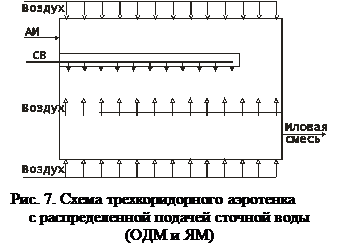
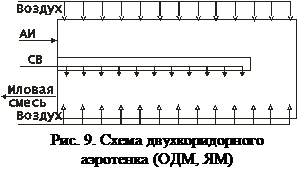
предполагает, что поток движется в режиме идеального вытеснения, но в нем происходит продольное перемешивание (рис. 7).

Ячеечная модель:

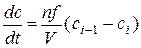(1.5)

основывается на том, что движущийся поток рассматривается состоящим из ряда последовательно соединенных ячеек. При этом приниматься, что в каждой ячейке поток имеет структуру идеального перемешивания, а между ячейками перемешивание отсутствует. Ректификационная колонна может быть описана ячеечной моделью.

Определение пара-метров МИП и МИВ не представляет особой труд-ности, так как сводится к расчетам коэффициентов дифференциальных уравне-ний по известным конструк-тивным и режимным параметрам.

Лекция 3