Интерпретация моделей авторегрессии
Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Например, потребление в момент времени t формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например потребления в период (t — 1). Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии.
Пусть имеется следующая модель:
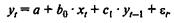
Как и в модели с распределенным лагом, b0 в этой модели характеризует краткосрочное изменение yt под воздействием изменения хt на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные. К моменту времени (t + 1) результат 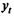 изменился под воздействием изменения изучаемого фактора в момент времени t на
изменился под воздействием изменения изучаемого фактора в момент времени t на 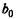 ед., а
ед., а 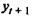 под воздействием своего изменения в непосредственно предшествующий момент времени — на с1 ед. Таким образом, общее абсолютное изменение результата в момент (t + 1) составит
под воздействием своего изменения в непосредственно предшествующий момент времени — на с1 ед. Таким образом, общее абсолютное изменение результата в момент (t + 1) составит  ед. Аналогично в момент времени (t + 2) абсолютное изменение результата составит
ед. Аналогично в момент времени (t + 2) абсолютное изменение результата составит 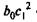 ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов:
ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов:
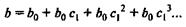
Учитывая, что практически во все модели авторегрессии вводится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной 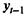 по абсолютной величине меньше единицы(|c1| < 1), соотношение (7.8) можно преобразовать следующим образом:
по абсолютной величине меньше единицы(|c1| < 1), соотношение (7.8) можно преобразовать следующим образом:
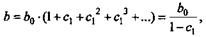 где
где 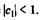
Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения
Дата добавления: 2015-08-01; просмотров: 834;
